Learning Structured Sparsity in Deep Neural Networks

发表于 更新于 分类于
本文字数： 4.9k 阅读时长 ≈ 9 分钟

原文地址：Learning Structured Sparsity in Deep Neural Networks

官方实现：wenwei202/caffe

复现地址：ZJCV/SSL

摘要

High demand for computation resources severely hinders deployment of large-scale Deep Neural Networks (DNN) in resource constrained devices. In this work, we propose a Structured Sparsity Learning (SSL) method to regularize the structures (i.e., filters, channels, filter shapes, and layer depth) of DNNs. SSL can: (1) learn a compact structure from a bigger DNN to reduce computation cost; (2) obtain a hardware-friendly structured sparsity of DNN to efficiently accelerate the DNNs evaluation. Experimental results show that SSL achieves on average 5.1x and 3.1x speedups of convolutional layer computation of AlexNet against CPU and GPU, respectively, with off-the-shelf libraries. These speedups are about twice speedups of non-structured sparsity; (3) regularize the DNN structure to improve classification accuracy. The results show that for CIFAR-10, regularization on layer depth can reduce 20 layers of a Deep Residual Network (ResNet) to 18 layers while improve the accuracy from 91.25% to 92.60%, which is still slightly higher than that of original ResNet with 32 layers. For AlexNet, structure regularization by SSL also reduces the error by around ~1%. Open source code is in this https URL

对计算资源的高需求严重阻碍了大规模深度神经网络（DNN）在资源受限设备中的应用。在这项工作中，我们提出了一种结构化稀疏学习（SSL）方法来调整DNNs的结构（比如滤波器、通道、滤波器形状和层深度）。SSL可以：（1）从一个较大的DNN中学习到一个紧凑的结构，从而减少计算量；(2）能够获得一种硬件友好的结构稀疏DNN，有效地加速DNN的推理。实验结果表明，通过SSL，AlexNet在CPU和GPU中的卷积层计算上平均加速了5.1x和3.1x。这个结果大概是非结构化稀疏方法加速的两倍；(3） 对DNN结构进行正则化能够提高分类精度。结果表明，对于CIFAR-10，基于层深度进行正则化计算，能够将深度残差网络（ResNet）减少20层深度，仅需18层，而精度由91.25%提高到92.60%，仍略高于原始ResNet的32层精度。对于AlexNet而言，SSL得到的结构正则化结果也减少了约1%的误差。开源代码位于https://github.com/wenwei202/caffe/tree/scnn

引言

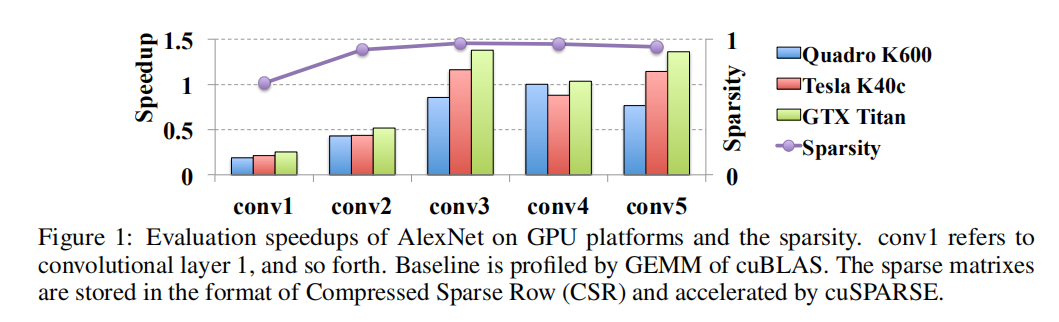
论文讨论了非结构化稀疏方法以及低秩近似方法的优缺点：

  1. 非结构化稀疏方法。以L1-norm为例
    1. 在训练过程中对每层权重额外添加L1-norm损失；训练完成后，对逐层权重进行阈值过滤，小于阈值的权重设置为0。从而得到稀疏网络；
    2. 在实际计算过程中，非结构化稀疏并不能真正带来加速效果。以上图为例，逐层实际加速效果并不与稀疏比率成正比，有些层执行速度反而下降了。
  2. 低秩近似方法。
    1. 首先进行正常的模型训练；完成训练后分解每层权重矩阵，用较小因子的乘积进行逼近；最后通过微调方式恢复损失精度；
    2. 低秩近似方法能够获得实际加速。不过需要通过大量实验进行矩阵分解和微调训练，训练难度大。

SSL

论文首先给出一个通用的结构化稀疏训练公式，然后分别基于滤波器、通道、滤波器形状以及层深度进行结构化稀疏实现，最后还讨论了其他一些变体。

通用公式

假定DNN由一系列4-D张量组成：\(W^{(l)} \in \Re^{N_{l}\times C_{l}\times M_{l}\times K_{l}}\)，其中

  • \(l\)表示第几个卷积层，\(1\leq l\leq L\)；
  • \(N\)表示滤波器个数；
  • \(C\)表示通道个数；
  • \(M\)表示滤波器空间高；
  • \(K\)表示滤波器空间宽。

对DNN进行结构化稀疏训练，其目标函数定义如下：

\[ E(W) = E_{D}(W) + \lambda\cdot R(W) + \lambda_{g}\cdot \sum_{l=1}^{L}R_{g}(W^{(l)}) \]

  • \(W\)表示DNN所有的权重集合；
  • \(E_{D}(W)\)表示基于数据计算得到的损失；
  • \(R(\cdot)\)表示对每个权重进行非结构化训练的正则化损失，比如L2-norm；
  • \(R_{g}(\cdot)\)表示对每层应用的结构化稀疏正则化损失。

在论文中，使用group lasso实现\(R_{g}(\cdot)\)，其表示如下：

\[ R_{g}(w) = \sum_{g=1}^{G}\left \| w^{(g)} \right \|_{g} \]

  • \(w\)表示一个权重集合，比如单个卷积层的权重矩阵；
  • \(w^{(g)}\)表示\(w\)中的一组权重；
  • \(G\)表示分组个数；
  • \(\left \| \cdot \right \|_{g}\)表示group lasso，其完整实现如下

\[ \left \| w^{(g)} \right \|_{g} = \sqrt{\sum_{i=1}^{\left | w^{(g)} \right |} (w_{i}^{(g)})^{2} } \]

  • \(\left | w^{(g)} \right |\)表示\(w^{g}\)的权重个数

特定公式

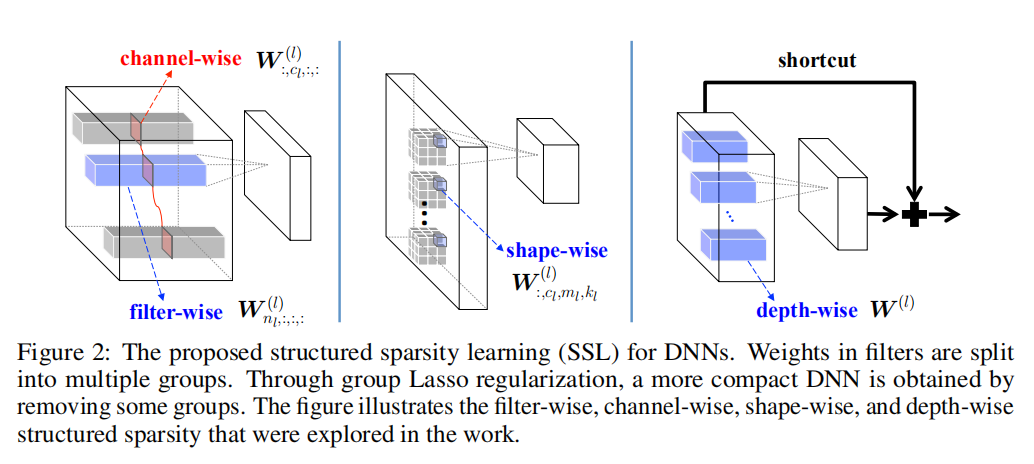
论文探索了4种结构化稀疏方式，如上图所示，分别是基于滤波器、基于通道、基于滤波器形状和基于层深度。

在后续公式中，忽略了正则化损失\(R(\cdot)\)

filter/channel

对于第\(l\)层的滤波器而言

  • \(W^{(l)}_{n_{l},:,:,:}\)表示第\(n_{l}\)个滤波器；
  • \(W^{(l)}_{:,c_{l},:,:}\)表示第\(c_{l}\)个滤波器。

其目标函数实现如下：

\[ E(W) = E_{D}(W) + \lambda_{n}\cdot \sum_{l=1}^{L} (\sum_{n_{l}=1}^{N_{l}} \left \| w^{(l)}_{n_{(l)},:,:,:} \right \|_{g}) + \lambda_{c}\cdot \sum_{l=1}^{L} (\sum_{c_{l}=1}^{C_{l}} \left \| w^{(l)}_{:,c_{l},:,:} \right \|_{g}) \]

  • \(\lambda_{n}\)表示超参数，控制滤波器正则化损失；
  • \(\lambda_{c}\)表示超参数，控制通道正则化损失；

因为上一层的滤波器维度就是下一层的通道维度，所以对滤波器和通道的稀疏化同时进行

filter shape

对于第\(l\)层的滤波器而言

  • \(W^{(l)}_{:,c_{l},m_{l},k_{l}}\)表示滤波器滤波器形状

其目标函数实现如下：

\[ E(W) = E_{D}(W) + \lambda_{s}\cdot \sum_{l=1}^{L} (\sum_{c_{l}=1}^{C_{l}} \sum_{m_{l}=1}^{M_{l}} \sum_{k_{l}=1}^{K_{l}} \left \| w^{(l)}_{:,c_{l},m_{l},k_{l}} \right \|_{g}) \]

  • \(\lambda_{s}\)表示超参数，控制滤波器形状正则化损失

layer depth

基于层深度进行结构化稀疏训练的损失函数如下：

\[ E(W) = E_{D}(W) + \lambda_{d}\cdot \sum_{l=1}^{L}\left \| W^{(l)} \right \|_{g} \]

  • \(\lambda_{d}\)表示超参数，控制层深度正则化损失

为了避免训练过程中某几层完全稀疏化之后无法将激活特征图传递到后续网络中，需要修改层结构，逐层实现残差连接，训练过程中不对一致性连接执行稀疏化训练

实验

论文在不同数据集（MNIST/CIFAR10/ImageNet）和不同模型（LeNet/AlexNet/ResNet）上进行了测试，均取得了加速推理的效果。

层深度剪枝

论文使用ResNet-20和ResNet-32进行了层深度实验（基于CIFAR10数据集），其结果下图所示：

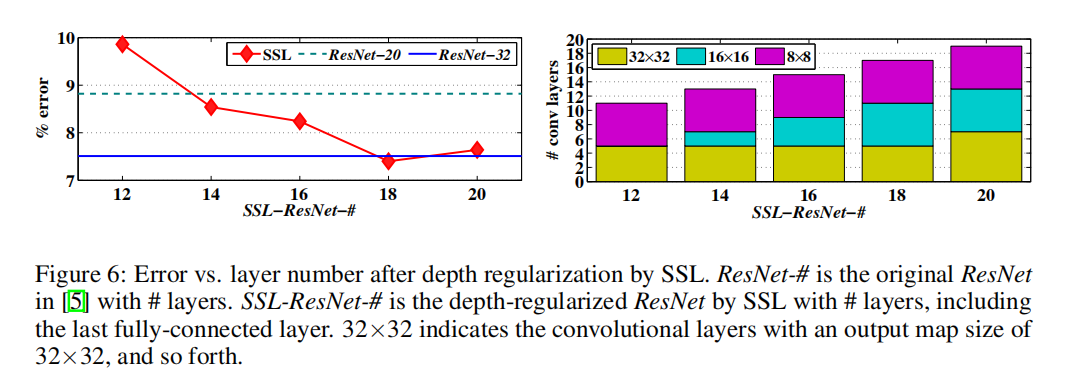
Sparsity/Speedup

论文使用AlexNet调查了逐层卷积在剪枝前后的变化（基于ImageNet数据集），同时与非结构化稀疏方法比较了加速能力，其结果如下图所示：

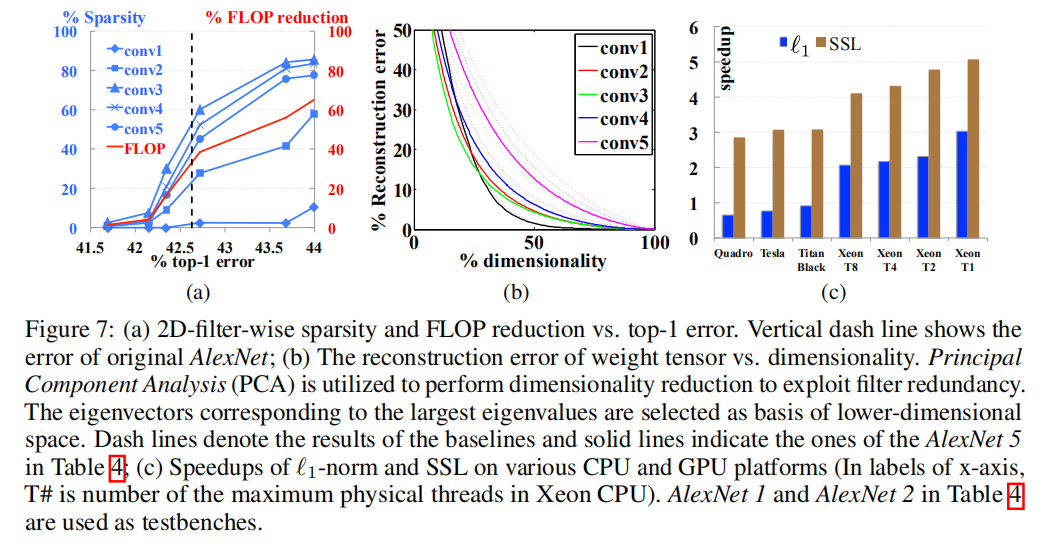
  • 从左图可知，更深的卷积层具有更高的稀疏比率。一方面是因为浅层卷积层本身参数量少；另一方面也说明了维持模型性能还是需要一定的参数量的；
  • 从右图可知，基于group lasso的SSL算法能够实现更高的加速能力。

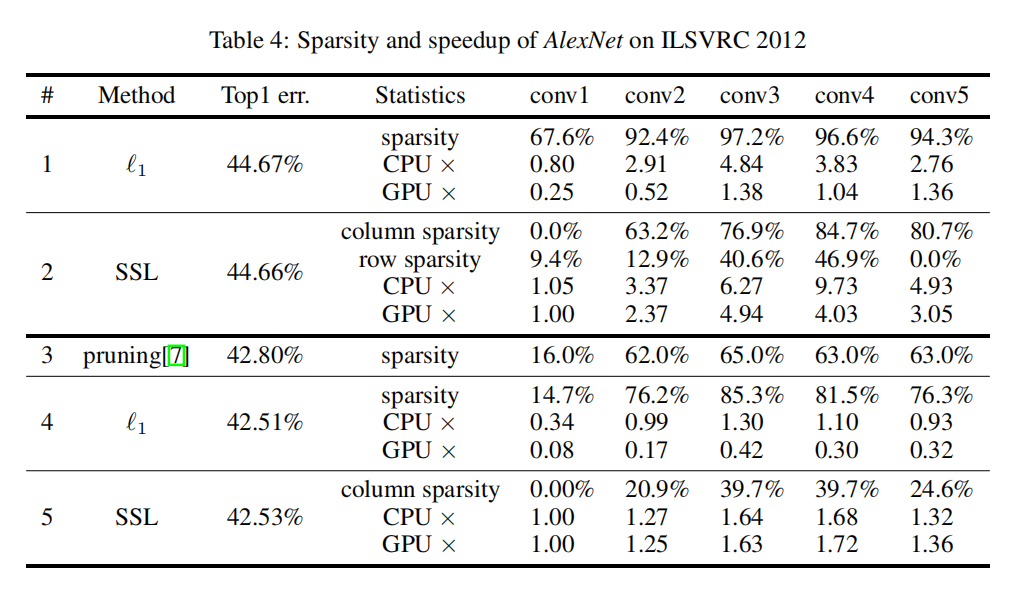
关于AlexNet在ImageNet上进行稀疏化训练，分别基于L1-norm和SSL的逐层稀疏和加速细节如下图所示：

实现

论文在官方实现上给出了一些实现技巧：

  1. 设置SSL训练和微调训练的基准学习率为从头训练原始网络的基准学习率的0.1x；
  2. 设置SSL训练的最大迭代次数\(K\)是从头训练原始网络的最大迭代次数\(M\)的\(\frac{1}{2}\)，即\(K=\frac{M}{2}\)；
  3. 设置微调训练的最大迭代次数\(N\)是\(M\)的\(\frac{1}{3}\)，即\(N=\frac{M}{3}\)；
  4. 在SSL训练阶段，初始学习率对于稀疏的作用非常大，所以需要更长的训练次数，在\(0.7\cdot K\)的时候才开始第一次衰减；
  5. 完成训练后，将小于\(1e^{-4}\)的权重设置为\(0\)

小结

整篇论文结构上简单清晰，利用group lasso对不同结构进行稀疏化训练，均能够实现结构化剪枝效果。在这其中，我对于层剪枝方式最感兴趣，一方面是因为之前没有看到过其他层剪枝论文；另一方面也是觉得这篇论文提出的层剪枝方式简单易行。

实现思路：

  • 关于滤波器/通道剪枝
    • 对第一个滤波器的通道维度不进行剪枝训练，因为输入数据和输出类别数固定；
    • 完成剪枝训练后，需要综合考虑当前层的滤波器剪枝个数以及下一层的通道剪枝个数，保证剪枝前后模型能够正常运行；
  • 关于层剪枝
    • 需要调整层结构，逐层实现残差结构；
    • 对于每层的一致性连接，不执行稀疏训练，仅对残差连接执行层稀疏训练。

小小猜想：

  • 单独进行滤波器剪枝和通道剪枝的效果咋样，和组合剪枝（滤波器＋通道）的比较如何；
  • 结合更多种稀疏策略一起实现会如何，比如同时进行滤波器+通道+层剪枝。当前这种方式很容易就导致剪枝训练的模型精度不高（因为稀疏化参数过多，导致模型性能下降）；
  • 或者我们可以逐步执行多种稀疏策略，比如先进行层剪枝，微调恢复精度后再执行滤波器/通道剪枝（也可以是其他论文中的剪枝方法）。

相关阅读