Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour

发表于 更新于 分类于
本文字数： 3.4k 阅读时长 ≈ 6 分钟

原文地址：Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour

摘要

Deep learning thrives with large neural networks and large datasets. However, larger networks and larger datasets result in longer training times that impede research and development progress. Distributed synchronous SGD offers a potential solution to this problem by dividing SGD minibatches over a pool of parallel workers. Yet to make this scheme efficient, the per-worker workload must be large, which implies nontrivial growth in the SGD mini-batch size. In this paper, we empirically show that on the ImageNet dataset large minibatches cause optimization difficulties, but when these are addressed the trained networks exhibit good generalization. Specifically, we show no loss of accuracy when training with large minibatch sizes up to 8192 images. To achieve this result, we adopt a hyper-parameter-free linear scaling rule for adjusting learning rates as a function of minibatch size and develop a new warmup scheme that overcomes optimization challenges early in training. With these simple techniques, our Caffe2-based system trains ResNet-50 with a minibatch size of 8192 on 256 GPUs in one hour, while matching small minibatch accuracy. Using commodity hardware, our implementation achieves ∼90% scaling efficiency when moving from 8 to 256 GPUs. Our findings enable training visual recognition models on internet-scale data with high efficiency.

深度学习在大型神经网络和大型数据集中蓬勃发展。然而，更大的网络和更大的数据集导致更长的训练时间，阻碍了研究和开发的进展。分布式同步SGD通过将SGD小批量划分到一个并行工作池上，为解决这个问题提供了一个潜在的解决方案。然而，要使此方案有效，每个工作线程的工作负载必须很大，这意味着SGD小批量的大小可以快速增长。在本文中，我们的经验表明，在ImageNet数据集上，大尺度的小批量会导致优化困难，但是当这些问题得到解决时，训练的网络表现出良好的泛化能力。通过实验证明了当每次训练高达8192张图片时，仍旧没有准确性损失。为了达到这一目的，我们采用了一种无超参数线性缩放规则，根据批量数目来调整学习率，并开发了一种新的warmup方案，克服了早期训练中的优化挑战。通过这些简单的技术，我们基于Caffe2的系统能够在一小时内在256 GPUs上训练ResNet-50，其小批量大小为8192，同时训练结果匹配批量更小数目时的精度。使用商用硬件，我们完成了从8 GPU切换到256 GPU的训练，并实现了近90%的扩展效率。我们的研究结果使得在互联网规模的数据上高效地训练视觉识别模型成为可能

章节内容

论文对如何在训练更大规模的模型和训练数据时保证训练时间可控的问题上进行了探究，证明了分布式同步随机梯度下降(SGD)大规模训练的可行性，并给出了实用的经验

  • 首先介绍了大尺度训练下的学习率调整：线性缩放规则以及warmup策略
  • 其次训练过程中常见的陷阱以及触发这些陷阱的实现细节
  • 然后详细的描述了分布式训练算法
  • 最后通过实验证明了大尺度训练的困难在于优化问题

线性缩放规则

Linear Scaling Rule: When the minibatch size is multiplied by k, multiply the learning rate by k.

线性缩放规则：当批量大小乘以\(k\)时，学习率同样乘以\(k\)（其余参数保持不变）

证明

论文通过数学假设证明了上述规则的有效性：比较批量大小为\(B_{j}\)的\(k\)轮SGD训练和批量大小为\(\cup_{j} B_{j}\)的\(1\)轮\(SGD\)训练

\[ w_{t+k} = w_{t} - \eta \frac {1}{n} \sum_{j<k} \sum_{x\in B_{j}} \triangledown l(x, w_{t+j}) \\ \hat{w}_{t+1} = w_{t} - \hat{\eta} \frac {1}{kn} \sum_{j<k} \sum_{x\in B_{j}} \triangledown l(x, w_{t}) \]

假定$ l(x, w_{t+j}) l(x, w_{t})\(，那么当\) = k\(时，能够判定两者基本训练一致（\)w_{t+k} _{t+1}$）

缺陷

存在两种情况下假定（$ l(x, w_{t+j}) l(x, w_{t})$）不符合

  1. 初期训练时网络权重快速变化阶段
  2. 批量大小不能够无限扩大

解决方案

  1. 对于第一个问题，通过warmup策略解决
  2. 对于第二个问题，通过实验证明了其训练尺度上限接近于8k

warmup策略

  • constant warmup
    • 原理：在前\(5\)轮训练中使用固定的小学习率进行训练
    • 适用场景：预训练模型微调训练
  • gradual warmup
    • 原理：在前\(5\)轮训练中，从一个较低的学习率\(\eta\)开始，然后逐渐增长到目标学习率\(k\eta\)
    • 适用场景：从头开始训练模型

BN大小

论文通过推导证明了每个GPU上的批量大小对于BN操作非常关键，保证每次训练时每个GPU上的训练数固定，有利于最后的模型准确度。论文同时证明了\(n=32\)（每个\(GPU\)上的批量大小）是一个很好的训练参数

实践指南

论文针对分布式训练过程中出现的各种实现陷阱，给出了具体的实践建议

  1. 缩放交叉熵损失不等于缩放学习率
  2. 如果使用动量替代公式，那么改变学习速率后同样需要进行动量修正
  3. 用总的批量大小\(kn\)，而不是每个GPU的批量大小\(n\)来标准化每个GPU上的损失
  4. 在每一轮训练中，使用同一次随机打乱的训练数据，然后划分到各个GPU进行训练

动量SGD的参考实现：

\[ u_{t+1} = mu_{t} + \frac {1}{n} \sum_{x\in B} \triangledown l(x, w_{t})\\ w_{t+1} = w_{t} - \eta u_{t+1} \]

为了简化实现，将\(v_{t}=\eta u_{t}\)代入得到以下实现：

\[ v_{t+1} = mv_{t} + \eta \frac {1}{n}\sum_{x\in B}\triangledown l(x, w_{t}) \\ w_{t+1} = w_{t} - v_{t+1} \]

需要对第一个公式（\(v_{t+1}=...\)）乘以动量校正因子\(\frac {\eta_{t+1}}{\eta}\)

实验

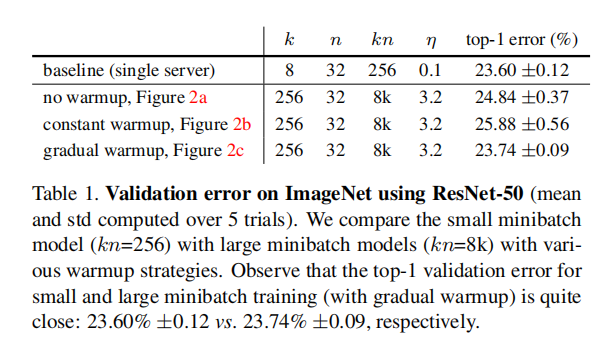
warmup

论文比较了不同warmup策略下的训练曲线和结果，证明了gradual warmup的有效性

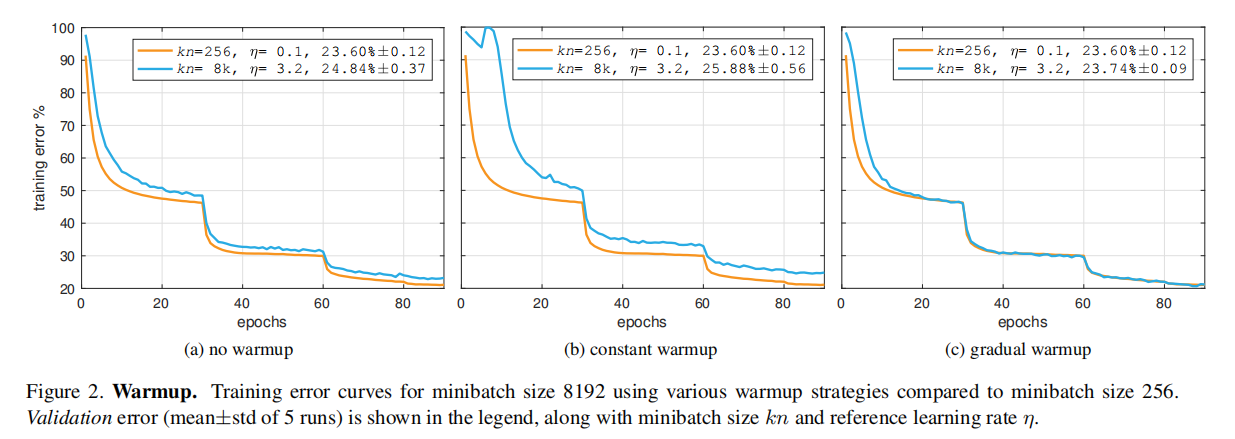
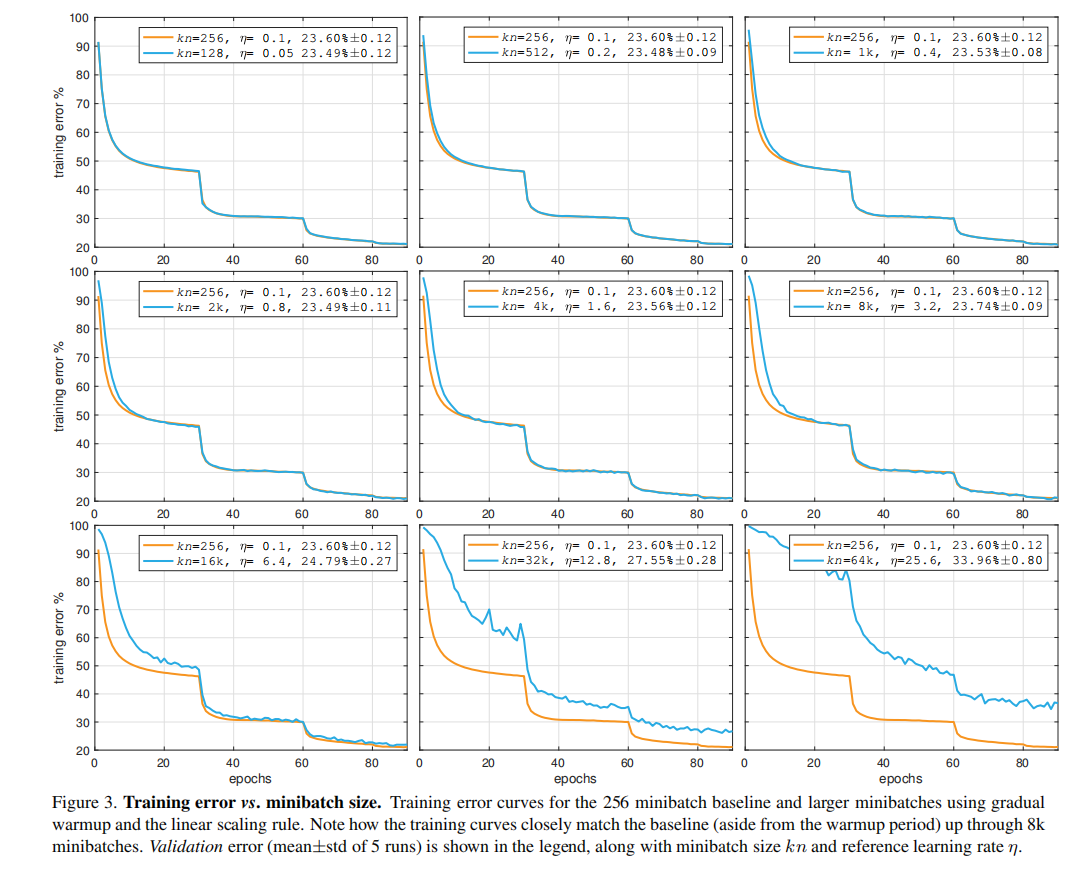
批量大小

论文比较了大尺度批量训练和256大小批量训练的训练曲线，证明了批量大小存在上界

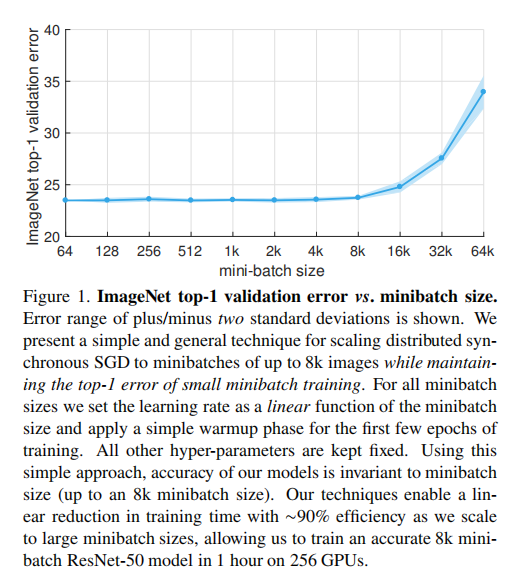
学习率

论文比较了不同的学习率训练结果，证明了线性缩放规则的有效性

相关阅读