凸函数

发表于 2019-04-27 更新于 2025-12-15 分类于技术教程，知识管理，基础教程，概念辨析阅读次数：本文字数： 459 阅读时长 ≈ 2 分钟

在机器学习和深度学习中，通常需要把目标函数设置或者假定为凸函数（Convex Function），这样能够满足局部最小值就是全局最小值的特点，方便进行梯度计算

局部最小值和全局最小值

局部最小值：如果存在一个，使得对于任意满足$\left|x-x^{}\right|<\varepsilon $的$ x $都有$ f\left(x^{}\right) \leq f(x) $，就把点$ x^{} $对应的函数值$ f(x^{}) $成为函数$ f$的一个局部最小值。从函数图像上看，局部最小值就像是山谷的一个底部
全局最小值：如果$x^{} $对于任意的$ x $都满足$ f\left(x^{}\right) \leq f(x) $，则称$ f(x^{*}) $为函数$ f$的全局最小值

凸函数定义

凸函数是一个定义在某个向量空间的凸子集上的实值函数，而且对于凸子集中任意两个向量、有成立

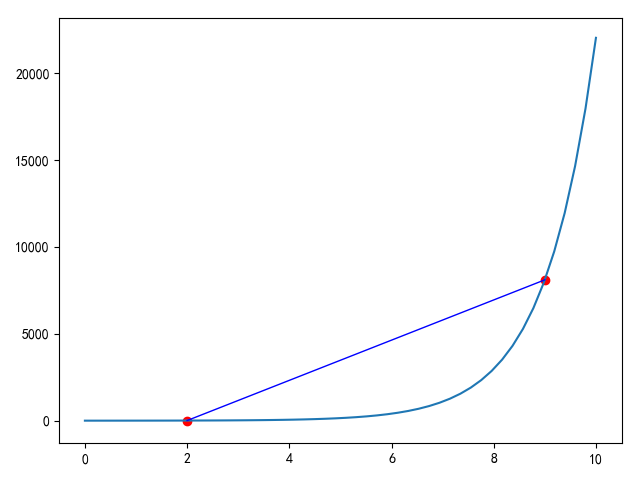
将凸子集改为某个区间，定义如下：设为定义在区间上的函数，若对上任意两点、和任意的实数，总有，则称为上的凸函数，若定义中的改为也成立，则称函数为对应子集或区间上的严格凸函数

如下图所示

from matplotlib.lines import Line2D
import matplotlib.pyplot as plt
import numpy as np

if __name__ == '__main__':
    x = np.linspace(0, 10)
    y = np.power(np.e, x)
    spots = [[2, np.power(np.e, 2)], [9, np.power(np.e, 9)]]
    (line1_xs, line1_ys) = zip(*spots)

    figure, ax = plt.subplots()
    ax.plot(x, y)
    plt.scatter(line1_xs, line1_ys, color='r')
    ax.add_line(Line2D(line1_xs, line1_ys, linewidth=1, color='b'))

    plt.show()

相关阅读

局部最小值