卷积神经网络推导-单张图片矩阵计算

发表于 更新于 分类于 阅读次数： 本文字数： 4.7k 阅读时长 ≈ 17 分钟

以LeNet-5为例，进行卷积神经网络的矩阵推导

计算符号

参考lecun-98，卷积层标记为，池化层标记为，全连接层标记为，比如表示第一层是卷积层

LeNet-5简介

LeNet-5共有7层（不包含输入层）

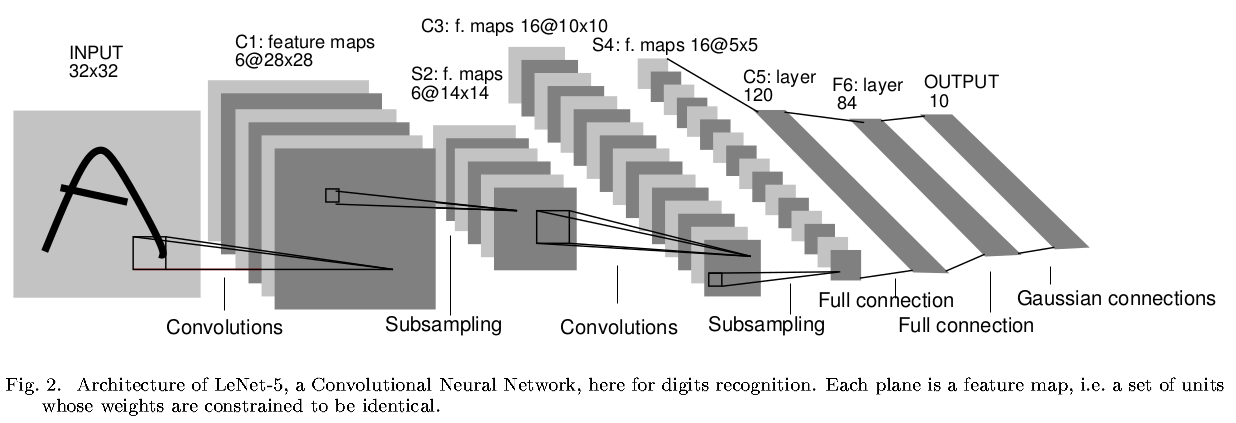
  • 有6个滤波器，感受野尺寸为，步长为，零填充为，所以共有个训练参数，输出激活图尺寸为

  • 感受野大小为，步长为，将输入数据体4个神经元相加后乘以一个可训练参数，再加上一个偏置值，最后进行操作，所以共有个训练参数，输出激活图尺寸为

  • 有16个滤波器，感受野尺寸为，步长为, 零填充为，所以输出激活图尺寸为

    • 的滤波器没有和完全连接：前6个滤波器和连续的3个激活图交互，接下来6个滤波器和连续的4个激活图交互，接下来3个滤波器和不连续的4个激活图交互，最后一个滤波器和全连接
    • 的参数个数是

  • 和一样，所以共有个可学习参数，输出激活图尺寸为

  • 有120个滤波器，感受野大小为，步长为，零填充为，所以共有个参数，输出激活图尺寸为，输出大小为

  • 有84个神经元，激活函数是，参数个数是个训练参数

  • 有10个神经元，得到84个输入后，不再执行点积运算，而是执行欧氏径向基函数（euclidean radial basis function）：

  • 损失函数是均方误差（Mean Squared Error, MSE）

最早的LeNet-5在1998年提出，经过多年发展，一些实现细节发生了变化，其中一个版本如下

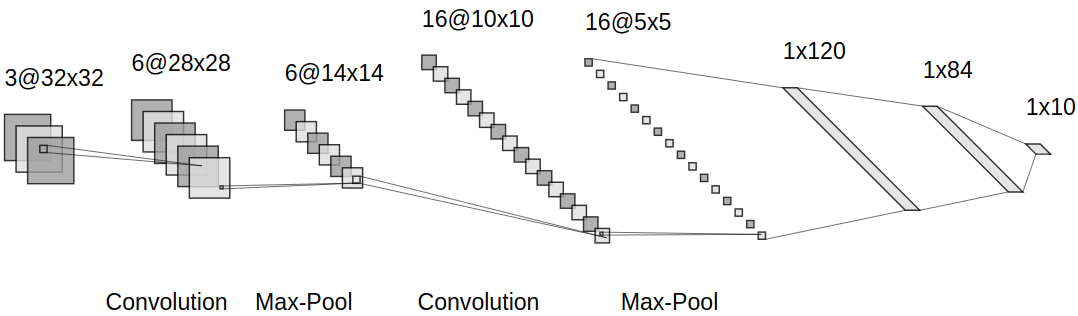
  • 有6个滤波器，感受野尺寸为，步长为，零填充为，激活函数是，所以共有个训练参数，输出激活图尺寸为

  • 感受野大小为，步长为，使用运算，所以输出激活图尺寸为

  • 有16个滤波器，感受野尺寸为，步长为, 零填充为，激活函数是，所以参数个数是，输出激活图尺寸为

  • 和一样，步长为，使用运算，所以输出激活图尺寸为

  • 有120个滤波器，感受野大小为，步长为，零填充为，激活函数为，所以共有，输出激活图尺寸为，输出大小为

  • 有84个神经元，激活函数是，参数个数是个训练参数，输出大小为

  • 有10个神经元，参数个数是个，输出大小为

  • 评分函数使用

  • 损失函数是交叉熵损失（Cross Entropy Loss）

输入 卷积核 步长 零填充 输出
C1 32x32x3 5x5 1 0 28x28x6
S2 28x28x6 2x2 2 \ 14x14x6
C3 14x14x6 5x5 1 0 10x10x16
S4 10x10x16 2x2 2 \ 5x5x16
C5 5x5x16 120 0 0 1x120
F6 1x120 84 \ \ 1x84
F7 1x84 10 \ \ 1x10

卷积层转全连接层

参考：Implementation as Matrix Multiplication

卷积层滤波器在输入数据体的局部区域执行点积操作，将每次局部连接数据体拉伸为行向量，那么卷积操作就等同于矩阵乘法，变成全连接层运算

比如输入图像大小为，卷积层滤波器大小为，步长为，零填充为，共有6个

那么等同于全连接层的输入维度为，共有个局部连接，所以矩阵运算如下：

得到输出数据后再拉伸回，就是下一层的输入数据体

池化层转全连接层

池化层滤波器在输入数据体的激活图上执行操作，将每次局部连接区域拉伸为行向量，同样可以将池化层操作转换成全连接层操作

比如输入数据体大小为，池化层滤波器空间尺寸，步长为

那么每次连接的向量大小是，每个激活图共有次局部连接，整个输入数据体共有次局部连接，所以运算如下：

得到输出数据后再拉伸回，就是下一层的输入数据体

矩阵计算

进行MNIST数据集的分类

前向传播

输入层

卷积层

共6个滤波器，每个滤波器空间尺寸为，步长为, 零填充为

输出空间尺寸为

所以单次卷积操作的向量大小为，单个滤波器有个局部连接

输出数据体

池化层

执行运算，每个滤波器空间尺寸，步长为

输出空间尺寸为

所以单次操作的向量大小为，单个滤波器有个局部连接

，每个值表示中每行最大值下标

输出数据体

卷积层

共16个滤波器，每个滤波器空间尺寸为，步长为, 零填充为

输出空间尺寸为

所以单次卷积操作的向量大小为，单个滤波器有个局部连接

输出数据体

池化层

执行运算，每个滤波器空间尺寸，步长为

输出空间尺寸为

所以单次操作的向量大小为，单个滤波器有个局部连接

，每个值表示中每行最大值下标

输出数据体

卷积层

共120个滤波器，每个滤波器空间尺寸为，步长为, 零填充为

输出空间尺寸为

所以单次卷积操作的向量大小为，单个滤波器有个局部连接

输出数据体

全连接层

神经元个数为

输出数据体

输出层

神经元个数为

输出数据体

分类概率

都是全向量

损失值

，仅有正确类别为1, 其余为0

反向传播

输出层

求输入向量梯度

其他梯度

求权重矩阵梯度

求偏置向量梯度

求上一层输出向量梯度

全连接层

求输入向量梯度

其他梯度

求权重矩阵梯度

求偏置向量梯度

求上一层输出向量梯度

卷积层

求输入向量梯度

其他梯度

求权重矩阵梯度

求偏置向量梯度

求上一层输出向量梯度

池化层

将梯度重置回梯度，再重置为梯度

因为卷积层滤波器的空间尺寸和的空间尺寸一致，所以不需要将先转换成，再转换成，可以一步到位

求输入向量梯度

上一层输出向量梯度

配合，最大值梯度和一致，其余梯度为

卷积层

将梯度重置回梯度，再重置为梯度

求输入向量梯度

$$
d(dataloss)
=tr(D_{y^{(3)}}f(y^{(3)})\cdot dy^{(3)})\
=tr(D_{y^{(3)}}f(y^{(3)})\cdot (1(z^{(3)} \geq 0)dz^{(3)}))\
=tr(D_{y^{(3)}}f(y^{(3)}) 1(z^{(3)} \geq 0)^{T}\cdot dz^{(3)})
$$

其他梯度

求权重矩阵梯度

求偏置向量梯度

表示的行数

求上一层输出向量梯度

池化层

输入层梯度大小为，是在输出数据体上采样获得，将重采样回梯度矩阵，再重置回大小，就是的梯度

上一层输出向量梯度

配合，最大值梯度和一致，其余梯度为

卷积层

将梯度重置回梯度，再重置为梯度

求输入向量梯度

$$
d(dataloss)
=tr(D_{y^{(1)}}f(y^{(1)})\cdot dy^{(1)})\
=tr(D_{y^{(1)}}f(y^{(1)})\cdot (1(z^{(1)} \geq 0)dz^{(1)}))\
=tr(D_{y^{(1)}}f(y^{(1)}) 1(z^{(1)} \geq 0)^{T}\cdot dz^{(1)})
$$

其他梯度

求权重矩阵梯度

求偏置向量梯度

表示的行数

相关阅读