批量归一化：通过减轻内部协变量偏移来加速深度网络训练
学习论文Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift，里面提出了批量归一化（Batch Normalization，简称BN）方法，一方面能够大幅提高训练速度，另一方面也能够实现更好的模型精度
摘要
Training Deep Neural Networks is complicated by the fact that the distribution of each layer’s inputs changes during training, as the parameters of the previous layers change. This slows down the training by requiring lower learning rates and careful parameter initialization, and makes it notoriously hard to train models with saturating nonlinearities. We refer to this phenomenon as internal covariate shift, and address the problem by normalizing layer inputs. Our method draws its strength from making normalization a part of the model architecture and performing the normalization for each training mini-batch. Batch Normalization allows us to use much higher learning rates and be less careful about initialization. It also acts as a regularizer, in some cases eliminating the need for Dropout. Applied to a state-of-the-art image classification model, Batch Normalization achieves the same accuracy with 14 times fewer training steps, and beats the original model by a significant margin. Using an ensemble of batchnormalized networks, we improve upon the best published result on ImageNet classification: reaching 4.9% top-5 validation error (and 4.8% test error), exceeding the accuracy of human raters.
训练深层神经网络是复杂的，因为每一层的输入分布在训练期间随着前一层的参数改变而改变。由于较低的学习率和精心的参数初始化，这降低了训练的速度，并且使得训练具有饱和非线性的模型变得非常困难。我们把这种现象称为内部协变量偏移，可以通过标准化层输入来解决这个问题。我们方法的优势在于将标准化作为模型架构的一部分，并对每个训练小批量执行数据标准化。批量归一化允许我们使用更高的学习率，并且不需要很关心初始化。它还起到了规范者的作用，在某些情况下消除了随机失活的需要。应用于最先进的图像分类模型，批量归一化以14倍的训练步骤实现了相同的精度，并且大大超过了原始模型。使用一组集成归一化网络，我们改进了ImageNet分类的最佳公布结果：达到4.9%的前5名验证错误(和4.8%的测试错误)，超过了人工评分者的准确性
什么是协变量偏移
在传统的深度学习模型训练过程中，需要对输入数据进行标准化预处理（零均值+很小方差），这样有利于后续的训练
但是当输入数据经过层计算后，输出数据可能不符合标准化分布，这种变化称之为内部协变量偏移（internal covariate shift）
协变量偏移影响
假设某一层执行如下：
\[ z=g(Wu+b) \]
其中\(u\)是输入，\(W\)是权重向量，\(b\)是偏置向量，\(g\)是\(sigmoid\)函数，实现如下:
\[ g(x) = \frac {1}{1+exp(-x)} \]
当\(\left | x \right |\)增大时，\({g}'(x)\)会趋向于\(0\)，参考：激活函数。也就是说，除了\(x\)很小的情况外，梯度将消失而导致训练变慢
\(x\)的大小受当前\(W\)和\(b\)以及之前层参数的影响，这些参数在训练过程中的改变会导致\(x\)的值进入激活函数的饱和区域，从而减缓了收敛速度，并且这种现象随网络深度增加而被放大
当输入数据分布发生变化后，层权重需要进一步调整以补偿这种变化，协方差偏移现象一方面会减慢训练过程，另一方面也不能保证训练结果能够实现最好精度
如何减轻内部协方差偏移
之前利用ReLU激活函数+精心的初始化+很小的学习率来减轻过饱和以及梯度消失的问题
文章提出批量归一化方法，对每层输入数据进行标准化预处理，保证输入数据符合标准化分布，以避免输出数据进入过饱和区域，从而避免梯度消失，加快模型收敛速度
BN层
前向传播
输入批量数据\(B={x_{1,...,m}}\)，BN层可学习参数\(\gamma, \beta\)
第一步：计算每个维度的期望和方差
\[ \mu_{B} = \frac {1}{m} \sum_{i=1}^{m}x_{i}\\ \sigma_{B}^{2} = \frac {1}{m} \sum_{i=1}^{m}(x_{i} - \mu_{B})^{2} \]
第二步：归一化输入数据
\[ \widehat{x_{i}} = \frac {x_{i} - \mu_{B}}{\sqrt{\sigma_{B}^{2} + \epsilon }} \]
$$是一个常量，避免标准差为0的情况
第三步：缩放和偏移标准化数据
\[ y_{i} = \gamma \widehat{x_{i}} + \beta \]
超参数\(\gamma\)初始化为\(1\)，\(beta\)初始化为\(0\)
反向传播
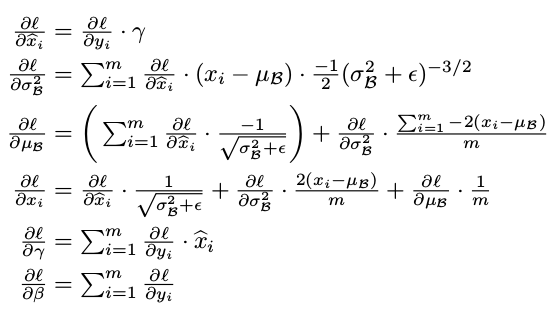
计算超参数\(\gamma\)和\(\beta\)梯度
\[ \frac {\partial l}{\partial \gamma} =\sum_{i=1}^{m} \frac {\partial l}{\partial y_{i}}\cdot \widehat{x_{i}} \]
\[ \frac {\partial l}{\partial \beta} =\sum_{i=1}^{m} \frac {\partial l}{\partial y_{i}} \]
计算中间标准化数据梯度
\[ \frac {\partial l}{\partial \widehat{x_{i}}} = \frac {\partial l}{\partial y_{i}}\cdot \gamma \]
计算均值和方差梯度
\[ \widehat{x_{i}} = \frac {x_{i} - \mu_{B}}{\sqrt{\sigma_{B}^{2} + \epsilon }} = (x_{i} - \mu_{B})(\sigma_{B}^{2} + \epsilon)^{-\frac {1}{2}} \]
\[ \Rightarrow \frac {\partial l}{\partial \sigma_{B}^{2}} =\sum_{i=1}^{m} \frac {\partial l}{\partial \widehat{x_{i}}}\cdot (x_{i} - \mu_{B})\cdot -\frac {1}{2}(\sigma_{B}^{2} + \epsilon)^{-\frac {3}{2}} \]
\[ \Rightarrow \frac {\partial l}{\partial \mu_{B}} =\frac {\partial l}{\partial \widehat{x_{i}}}\cdot \frac {\partial \widehat{x_{i}}}{\partial \mu_{B}} +\frac {\partial l}{\partial \sigma_{B}^{2}}\cdot \frac {\partial \sigma_{B}^{2}}{\partial \mu_{B}}\\ =\sum_{i=1}^{m} \frac {\partial l}{\partial \widehat{x_{i}}}\cdot \frac {-1}{\sqrt{\sigma_{B}^{2} + \epsilon }} +\frac {\partial l}{\partial \sigma_{B}^{2}}\cdot \frac {1}{m} \sum_{i=1}^{m}\cdot (-2(x_{i}-\mu_{B})) \]
计算输入数据梯度
\[ \frac {\partial l}{\partial x_{i}} =\frac {\partial l}{\partial \widehat{x_{i}}}\cdot \frac {\widehat{x_{i}}}{\partial x_{i}} +\frac {\partial l}{\partial \sigma_{B}^{2}}\cdot \frac {\partial \sigma_{B}^{2}}{\partial x_{i}} +\frac {\partial l}{\partial \mu_{B}}\cdot \frac {\partial \mu_{B}}{\partial x_{i}} =\frac{\partial l}{\partial \widehat{x_{i}}}\cdot \frac {1}{\sqrt{\sigma_{B}^{2} + \epsilon}} +\frac {\partial l}{\partial \sigma_{B}^{2}}\cdot \frac {2(x_{i}-\mu_{B})}{m}+\frac {\partial l}{\partial \mu_{B}}\cdot \frac {1}{m} \]
BN层作用
- 归一化输入数据的作用？
使得每次输入数据都保持相同的分布，减轻内部协变量偏移现象，加速训练过程
- 超参数\(\gamma\)和\(\beta\)的作用?
归一化输入数据会降低层的表达能力（因为输入数据的取值范围被限制了），使用超参数\(\gamma\)和\(beta\)进一步对归一化数据进行缩放和偏移，保证层的表达能力
比如对sigmoid输入数据进行归一化操作，其取值会限制在sigmoid的线性区域（[-1, 1]之间的sigmoid操作近似于直线）
使用超参数\(\gamma\)和\(beta\)保证了数据取值范围的扩大，极端情况下，设置\(\gamma^{(k)} = \sqrt{Var[x^{(k)}]}\)和\(\beta^{(k)}=E[x^{(k)}]\)能够恢复原始模型的激活状态
如果学习可学习参数\(\gamma\)和\(beta\)
文章中并没有介绍如何学习BN层的可学习参数\(\gamma\)和\(\beta\)，参考Batch normalization: How to update gamma and beta during backpropagation training step?，和权重向量一样，通过随机梯度下降方法进行更新即可
BN网络
将BN层插入到线性操作（卷积操作或全连接操作）之后，激活函数之前，如下所示：
因为BN层是可微的，所以按照正常的随机梯度下降方法进行训练，需要额外保存每次BN层计算的均值\(\mu_{B}\)和方差\(\sigma_{B}^{2}\)
在测试阶段，计算保存的均值期望和无偏方差期望
\[ E[x] = E_{B}[\mu_{B}]\\ Var[x] = \frac {m}{m-1}E_{B}[\sigma_{B}^{2}] \]
\(m\)表示批量个数
BN层操作如下：
\[ y =\gamma\cdot \frac{x - E[x]}{\sqrt{Var[x]+\epsilon}}+\beta =\frac{\gamma}{\sqrt{Var[x]+\epsilon}}\cdot x +(\beta - \frac {\gamma E[x]}{\sqrt{Var[x]+\epsilon}}) \]
参考
- 为什么要插入到非线性操作之前？
原因一：如果每层的输入数据\(a\)是上一层非线性输出的结果，其分布会在本层操作中改变，不能有效消除协变量偏移
原因二：相比于输入数据\(a\)（经过了非线性变换），\(W\cdot a+b\)是一个更对称，非稀疏的分布，对它进行归一化操作有利于得到稳定的分布
取消偏置向量\(b\)
因为在线性变换后，还会经过归一化操作，所以偏置向量\(b\)的作用被抵消了，其实现由超参数\(\beta\)完成，所以插入了\(BN\)层的网络可以忽略偏置向量\(b\)
\[ z = g(BN(W\cdot a)) \]
卷积层中的批量操作
为保留卷积层特性，逐特征图进行均值和方差计算（每个特征图向量属于一个属性），每个特征图都单独有一对\(\gamma ^{(k)}\)和\(\beta ^{(k)}\)
所以批量大小\(m\)等于图像个数乘以特征图大小
\[ {m}' = \left | B \right | = m\cdot pq \]
特征图大小\(p\times q\)
比如经过卷积操作后的数据体大小为\(128\times 16\times 10 \times 10\)，即批量大小为\(N = 128\)，滤波器个数为\(F = 16\)，特征图大小为\(p\times q = 10\times 10\)，所以\(\gamma\)和\(\beta\)大小为\(16\)
先转换数据体维度为\([N, F, p, q] \rightarrow [N, p, q, F]\)，再变形为\([N\times p\times q, F]\)，进行尺度缩放和偏移后最后转换回\([N, F, p, q]\)
BN网络额外作用
允许更高的学习率
在传统深度网络中，太高的学习率会导致梯度爆炸或消失，使得训练陷入局部最小值。使用批量归一化后，可以避免参数的微小变化被放大导致模型进入非线性饱和状态、 \[ BN(Wu) = BN((aW)u) \]
与此同时，权重变化与梯度变化呈反比 \[ \frac {\partial BN((aW)u)}{\partial u}=\frac {\partial BN(Wu)}{\partial u}\\ \frac {\partial BN((aW)u)}{\partial (aW)}=\frac {1}{a}\cdot \frac {\partial BN(Wu)}{\partial W} \]
所以权重增大后梯度变化变缓，需要更大的学习率才能够加速训练
批量归一化能够正则化模型，避免过拟合 批量归一化操作能够提高模型泛化作用，类似于随机失活操作，使用批量归一化后可以移除或降低随机失活强度
训练技巧
除了输入BN到网络外，文章提供了额外的训练技巧来帮助提高模型精度
- 更高的学习率
- 移除随机失活
- 减少\(L2\)权重正则化
- 加速学习率衰减
- 移除LRN
- 更彻底的打乱训练集，避免小批次数据集中总是出现相同的示例
- 减少光度畸变（应该是减小图像预处理操作）
小结
- 修复输入数据的均值和方差，减轻内部协变量影响
- 允许使用更高的学习率，避免参数爆炸
- 正则化模型，避免模型过拟合
- 允许使用饱和非线性激活函数