超参数优化
神经网络/卷积神经网络中存在很多的超参数,并且随着优化技术的发展,越来越多的超参数被加入进来,最常见的超参数包括:
- 初始学习率
- 学习率衰减机制(比如衰减常数)
- 正则化策略(
L2惩罚,随机失活强度)
大多数超参数在训练过程中相对固定,比如动量大小,衰减常数等,cs231n提出一些学习技巧来帮助搜索最佳的超参数值
实现
使用两个程序实现优化过程,worker程序持续采样随机超参数并执行优化。在训练过程中,worker程序持续追踪每一轮的验证集性能(或者其他数据集性能),写入一个模型检查点(包含了各种数据,包括损失值,精度值,权重向量等等)文件,文件名应该直接包含验证集精度值,以便后续的排序。master程序用于加载或杀死worker程序,通常额外包含查看检查点文件以及绘图功能
单验证集文件
通常情况在交叉验证(crosss-validation)某个参数时使用单个验证集即可,这样可以简化代码库实现
超参数范围
在对数尺度上搜索超参数。以学习率搜索为例,采样公式为learning_rate = 10 ** uniform(-6, 1),在均匀分布中采样随机数作为10的阶数,这种策略同样可用于正则化强度
如果学习率为0.001,那么固定增减0.01会发生很大影响;但是如果学习率是10,几乎没有影响。应该考虑对学习率乘以或者除以某个值,而不是在一定范围内增加或者减去某个值
对于某些超参数(比如随机失活)而言,还是应该使用正常尺度进行搜索(dropout = uniform(0,1))
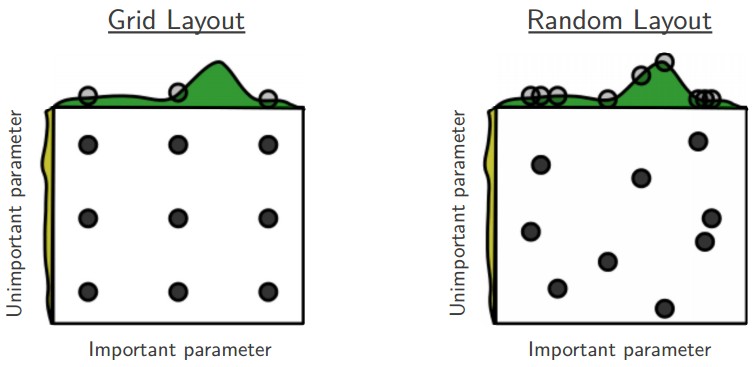
使用随机搜索而不是网格搜索
文章Random Search for Hyper-Parameter Optimization提出使用随机搜索更有利于超参数优化,同时更容易实现
注意边界上的最佳值
有些时候不一定能在指定范围内得到最佳的超参数,所以搜索得到超参数后应该再次检查该超参数值是否出现在边界,如果是,重设取值范围进行搜索
从粗到细进行搜索
可以划分不同阶段,先粗粒度搜索,再进行细粒度搜索。粗细阶段的划分有两个方面:
一个方面是在粗范围搜索过程中设置更大的取值,在细范围搜索过程中设置更小的取值
另一方面是在粗范围搜索过程中训练一次完整迭代(one epoch)甚至更少,然后随着阶段的深入逐渐提高训练迭代次数(1 -> 5 -> 50 -> ...)
贝叶斯超参数优化
贝叶斯(bayesian)超参数优化是一个研究领域,致力于提出更有效地导航超参数空间的算法。核心思想是在查询不同超参数下的性能时,适当平衡勘探开发权衡。当前有很多的模型库实现,不过在实际应用中其效果并不如随机搜索优化策略
小结
cs231n中更推荐使用随机搜索方式(配合粗细阶段设置)进行超参数优化