Rethinking the Value of Network Pruning
原文地址:Rethinking the Value of Network Pruning
摘要
Network pruning is widely used for reducing the heavy inference cost of deep models in low-resource settings. A typical pruning algorithm is a three-stage pipeline, i.e., training (a large model), pruning and fine-tuning. During pruning, according to a certain criterion, redundant weights are pruned and important weights are kept to best preserve the accuracy. In this work, we make several surprising observations which contradict common beliefs. For all state-of-the-art structured pruning algorithms we examined, fine-tuning a pruned model only gives comparable or worse performance than training that model with randomly initialized weights. For pruning algorithms which assume a predefined target network architecture, one can get rid of the full pipeline and directly train the target network from scratch. Our observations are consistent for multiple network architectures, datasets, and tasks, which imply that: 1) training a large, over-parameterized model is often not necessary to obtain an efficient final model, 2) learned “important” weights of the large model are typically not useful for the small pruned model, 3) the pruned architecture itself, rather than a set of inherited “important” weights, is more crucial to the efficiency in the final model, which suggests that in some cases pruning can be useful as an architecture search paradigm. Our results suggest the need for more careful baseline evaluations in future research on structured pruning methods. We also compare with the “Lottery Ticket Hypothesis” (Frankle & Carbin 2019), and find that with optimal learning rate, the “winning ticket” initialization as used in Frankle & Carbin (2019) does not bring improvement over random initialization.
网络剪枝被广泛用于减少低资源环境中深度模型巨大的推理成本。典型的剪枝算法可分为三阶段的流水线,即训练(大模型)、剪枝和微调。在剪枝过程中,根据一定的标准,冗余的权重被修剪,重要的权重被保留,从而尽可能的保持准确性。在这项工作中,我们得到几个令人惊讶的观察,这些观察与普遍的看法相矛盾。对于我们研究的所有最先进的结构化剪枝算法,微调一个剪枝模型只能得到与训练随机初始化权重的模型相当或更差的性能。对于采用预定义目标网络架构的剪枝算法,可以去掉整个流程直接从头开始训练目标网络。我们对多个网络架构、数据集和任务的观察是一致的,这意味着:1)训练一个大的、过度参数化的模型对于获得一个有效的最终模型通常是不必要的,2)学习大模型的“重要”权重对于小的剪枝模型通常是无用的,3)对于最终模型而言,剪枝架构本身比继承的“重要”权重更关键,这表明在某些情况下剪枝作为架构搜索范例是有用的。我们的结果表明,在未来关于结构化剪枝方法的研究中,需要更仔细的基线评估。我们还与“彩票假说”(Frankle & Carbin 2019)进行了比较,发现在最优学习率下,Frankle & Carbin (2019)中使用的“中奖彩票”初始化并没有带来比随机初始化更好的改进。
简介
这是一篇类综述性的文章,通过对当时最先进(2018年及之前)的剪枝论文的实验、观察和总结,发现剪枝算法的本质是网络架构搜索,而不是继承大模型的重要权重。
3阶段Pipeline
一个典型的网络剪枝算法可分为3个步骤进行:
- 训练一个大的、过度参数化的模型;
- 通过一个评判标准剪枝训练模型;
- 微调剪枝模型以获得最好的性能。
论文观点
之前的观点:
- 大模型拥有更强大的表示能力,能够安全的移除冗余参数而不损害性能,这通常被认为优于从零开始直接训练一个更小的网络;
- 剪枝算法的目标在于获取更小的剪枝架构以及相应的关键的权重值。如何选择关键的权重值也是一个重要的研究方向。
论文的观点:
- 对于拥有预定义目标剪枝架构的结构化剪枝算法(
predefined target network architectures)而言,直接通过随机初始化权重方式训练该目标架构比通过剪枝算法得到关键权重值后训练该架构能够得到相同甚至更好的性能; - 对于通过结构化剪枝算法搜索得到的目标架构(
auto-discovered target networks),从头开始训练也能得到比微调训练一样相近甚至更好的性能; - 对于非结构化剪枝算法
- 在小数据集上,从头开始训练剪枝模型能够得到和继承大模型关键权重后微调训练相近的性能;
- 在大数据集(比如
ImageNet)上,微调训练能够得到更好的性能。
对于结构化剪枝和非结构化剪枝的解释:
- 结构化剪枝:基于卷积通道或者更大的单位进行剪枝;
- 非结构化剪枝:基于卷积单个权重进行剪枝。
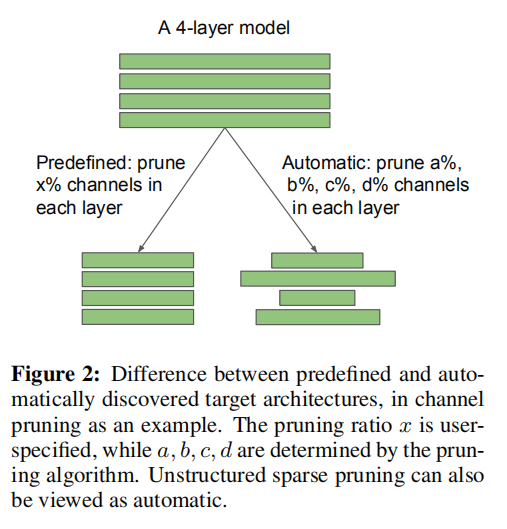
对于预定义目标架构和自动搜索目标架构的解释:
- 预定义目标架构:预先定义好每层通道的剪枝比例;
- 自动搜索目标架构:通过剪枝算法发现每层通道的剪枝比例。
章节概述
- 第二节:关于网络剪枝相关的背景和工作;
- 第三节:描述了从头开始训练剪枝模型的方法;
- 第四节:在不同剪枝算法上进行实验,展示了预定义目标剪枝架构和自动搜索目标架构的实验结果;
- 第五节:讨论自动剪枝算法在搜索高效的网络架构上的价值;
- 第六节:比较了最新提出的“彩票假说”;
- 第七节:讨论了一些含义并总结论文。
相关背景
- 结构化剪枝方法在通道甚至层的基础上进行剪枝。由于原始卷积结构仍然保留,因此不需要专用硬件/库来实现优化;
- 在结构化剪枝方法中,通道剪枝是最流行的,因为它在最细粒度的级别上运行,同时仍然适合传统的深度学习框架;
实验设置
关于训练资源,论文讨论了需要多长时间(训练轮数)来从头开始训练一个模型,使用了两种设置:
Scratch-E:训练小的剪枝模型需要和训练大的模型一样的轮数;Scratch-B:训练小的剪枝模型需要和训练大的模型一样的训练资源。比如在ImageNet数据集上,剪枝模型减少了2倍的Flops,那么训练轮数提高两倍。
关于其他设置:
- 剪枝模型的其他训练设置和大模型训练设置一样;
- 对于学习率衰减设置,基于实际训练轮数进行调整。
在后续的论文实验中,增加训练轮数(使用Scratch-B)很少是有害的,另外:
- 对大部分情况而言,使用
Scratch-E设置已经能够得到很好的结果; Scratch-B的训练结果往往比Scratch-E更好。
实验结果
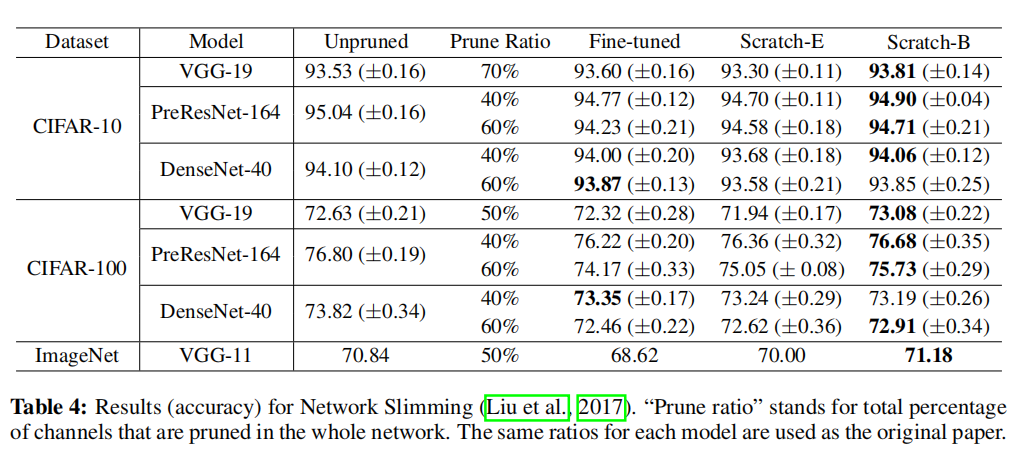
论文比较了基于预定义目标模型的结构化剪枝算法、自动搜索架构的结构化剪枝算法以及非结构化剪枝算法。从试验结果看,从头训练的剪枝模型均能够得到和微调一样甚至更好的性能。以Network Slimming为例:
架构搜索
论文还分析了使用剪枝算法进行架构搜索的作用,如下图所示:
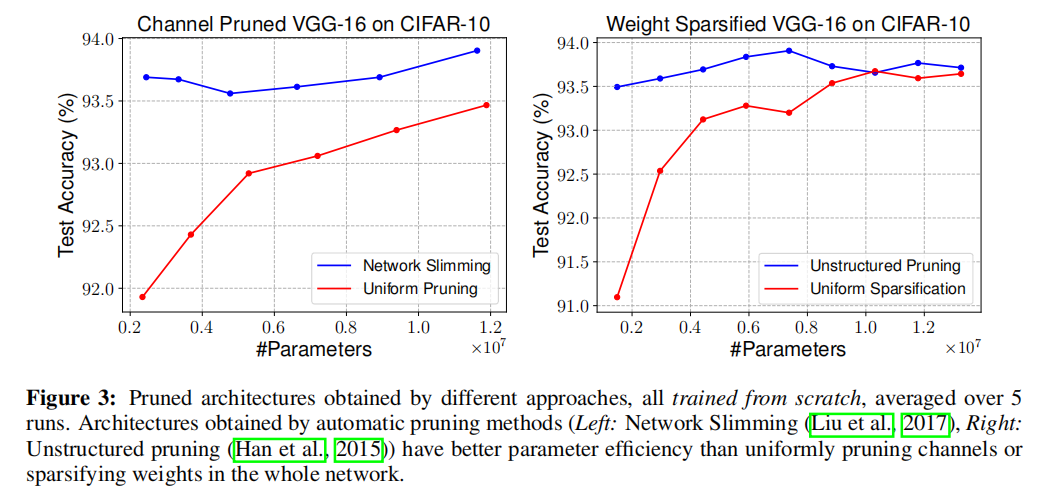
- 上图左侧展示了通过
Netowork Slimming和均匀通道剪枝(在每一层均匀的剪枝一定比例的通道数)的结果,从试验结果可以看到通过剪枝算法得到的剪枝模型的有效性; - 上图右侧展示了非结构化剪枝算法和均匀通道剪枝的比较,同样存在相同的现象。
论文还展示了剪枝算法得到的架构也存在某一排列模型,如下图所示:
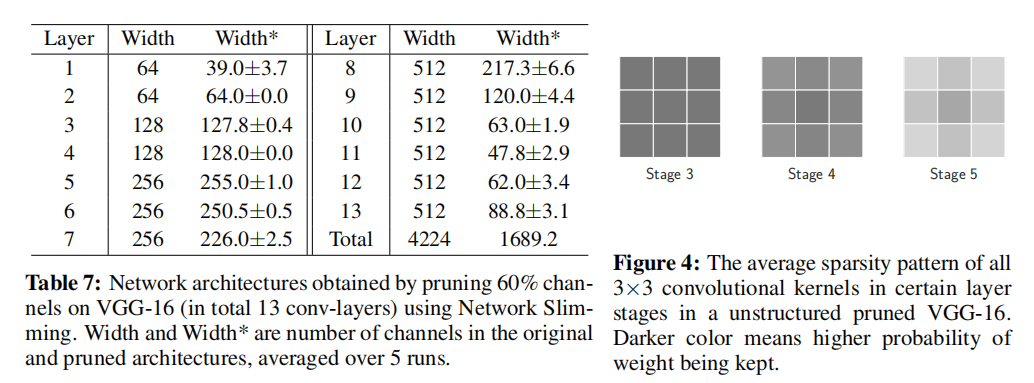
- 表7展示了架构化剪枝前后的各层的通道数;
- 图4展示了非结构化剪枝后每个阶段卷积核的平均稀疏模式。
从结果看,剪枝算法搜索到的架构也符合一定排列规则
论文也发现了通过剪枝算法得到的剪枝模型和均匀剪枝得到的剪枝模型拥有类似性能的实验,如下图所示:
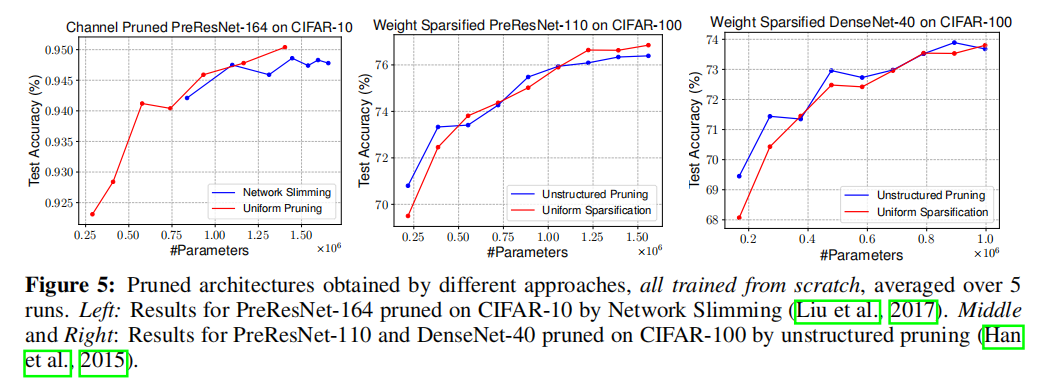
论文分析的一个原因是剪枝算法得到的剪枝模型在各层拥有相近的稀疏比例,这也是为什么剪枝算法和均匀剪枝拥有相近性能的原因
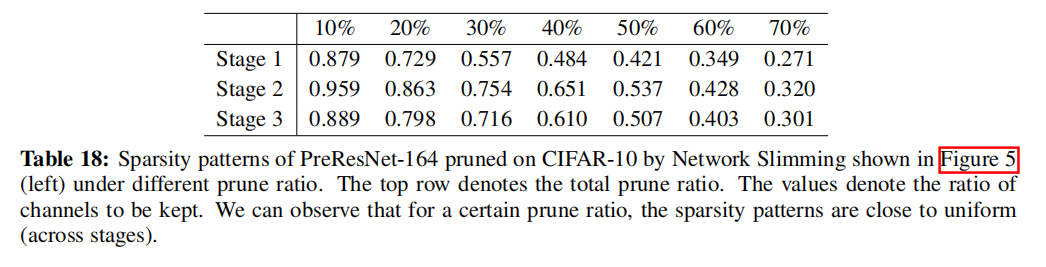
小结
论文通过详尽的实验讨论了剪枝模型微调权重的不必要性,证明了剪枝算法的关键在于搜索更高效的模型架构而不是识别关键权重。
一点猜想
- 既然剪枝算法类似于网络架构搜索,那么在某个数据集(小的)上得到的剪枝模型是否可以迁移到另一个数据集(大的)上呢?
- 论文也提到了剪枝模型也存在一定的设计规范,这个规范指出了模型冗余的地方,那么是否可以基于观察到的规范去设置更大的模型呢?