[二分类]PR曲线

发表于 更新于 分类于
本文字数： 4.9k 阅读时长 ≈ 9 分钟

PR曲线是另一种衡量算法性能的评价标准，其使用精确度（Precision, Y轴）和召回率（Recall, X轴）作为坐标系的基底

本文着重于二分类的PR曲线

参考一个例子：

Suppose a computer program for recognizing dogs in photographs identifies 8 dogs in a picture containing 12 dogs and some cats. Of the 8 identified as dogs, 5 actually are dogs (true positives), while the rest are cats (false positives). The program's precision is 5/8 while its recall is 5/12.

精确度

精确度（Precision）也称为正预测值（positive predictive value, PPV），表示预测为真的正样本占预测正样本集的比率

\[ PPV = \frac {TP}{TP + FP} \]

召回率

召回率（Recall）也称为敏感度（sensitivity）、真阳性率（true positive rate, TPR），表示预测为真的正样本占实际正样本集的比率

\[ TPR = \frac {TP}{TP + FN} \]

PR曲线

PPV和TPR两者都是对于预测为真的正样本集的理解和衡量

  • 高精度意味着算法预测结果中包含了更多的正样本（预测为真的正样本中有多少是对的，也就是查准率），但也可能存在预测为真的正样本占实际正样本集的比率不高的情况，这时会存在更多的假阴性样本，也就是正样本识别为负样本的情况；
  • 高召回率意味着算法预测结果能够更好的覆盖所有的正样本（找出来多少个正样本，也就是查全率），但也可能存在预测为真的正样本占预测正样本集的比率不高的情况，这时会存在更多的假阳性样本，也就是负样本识别为正样本的情况。

PR曲线是一个图，其y轴表示精度，x轴表示召回率，通过在不同阈值条件下计算(Recall, Precision)数据对，绘制得到PR曲线

根据定义可知，最好的预测结果发生在右上角(1,1)，此时所有预测为真的样本均为实际正样本，没有正样本被预测为负样本。

如何通过PR判断分类器性能 - AP

和ROC曲线类似，需要计算曲线下面积来评判分类器性能，称之为平均精度（AP, average precision）

\[ AP = \sum_{n}(R_{n} - R_{n-1})P_{n} \]

点\((R_{n}, P_{n})\)表示第\(n\)个阈值下的精度和召回率

Python实现

Python库Sklearn提供了PR曲线的计算函数：

average_precision_score

1
2
def average_precision_score(y_true, y_score, average="macro", pos_label=1,
                            sample_weight=None):

用于计算预测成绩的平均精度

  • y_true：数组形式，二值标签
  • y_score：目标样本的成绩
  • pos_label：正样本标签，默认为1
1
2
3
4
5
6
import numpy as np
from sklearn.metrics import average_precision_score

y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
average_precision_score(y_true, y_scores)

precision_recall_curve

1
2
def precision_recall_curve(y_true, probas_pred, pos_label=None,
                           sample_weight=None):

计算不同概率阈值下的精确率和召回率

  • y_true：数组形式，表示样本标签，如果不是{-1,1}或者{0,1}形式，那么属性pos_label应该指定
  • probas_pred：预测置信度
  • pos_label：正样本类，默认为1

返回3个数组，分别是精确率数组、召回率数组和阈值数组

1
2
3
4
5
6
import numpy as np
from sklearn.metrics import precision_recall_curve

y_true = np.array([0, 0, 1, 1])
y_scores = np.array([0.1, 0.4, 0.35, 0.8])
precision, recall, thresholds = precision_recall_curve(y_true, y_scores)

计算最佳阈值

综合来看，就是最接近坐标(1,1)的点所对应的阈值就是最佳阈值

1
best_th = threshold[np.argmax(precision + recall)]

示例

参考[二分类]ROC曲线使用Fashion-MNIST数据集，分两种情况

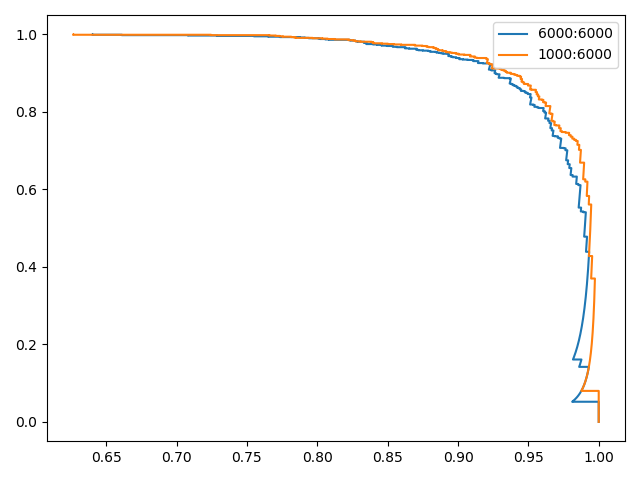
  1. 6000个运动鞋+6000个短靴作为训练集
  2. 1000个运动鞋+6000个短靴作为训练集

测试１

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
# -*- coding: utf-8 -*-

"""
@author: zj 
@file:   2-pr.py
@time:   2020-01-10
"""

from mnist_reader import load_mnist
from lr_classifier import LogisticClassifier
import numpy as np
from sklearn.metrics import precision_recall_curve
import matplotlib.pyplot as plt


def get_two_cate(ratio=1.0):
    path = "/home/zj/data/fashion-mnist/fashion-mnist/data/fashion/"
    train_images, train_labels = load_mnist(path, kind='train')
    test_images, test_labels = load_mnist(path, kind='t10k')

    num_train_seven = np.sum(train_labels == 7)
    num_train_nine = np.sum(train_labels == 9)
    # print(num_train_seven, num_train_nine)

    num_test_seven = np.sum(test_labels == 7)
    num_test_nine = np.sum(test_labels == 9)
    # print(num_test_seven, num_test_nine)

    x_train_0 = train_images[(train_labels == 7)]
    x_train_1 = train_images[(train_labels == 9)]
    y_train_0 = train_labels[(train_labels == 7)]
    y_train_1 = train_labels[(train_labels == 9)]

    x_train = np.vstack((x_train_0[:int(ratio * num_train_seven)], x_train_1))
    y_train = np.concatenate((y_train_0[:int(ratio * num_train_seven)], y_train_1))
    x_test = test_images[(test_labels == 7) + (test_labels == 9)]
    y_test = test_labels[(test_labels == 7) + (test_labels == 9)]

    return x_train, (y_train == 9) + 0, x_test, (y_test == 9) + 0


def compute_accuracy(y, y_pred):
    num = y.shape[0]
    num_correct = np.sum(y_pred == y)
    acc = float(num_correct) / num
    return acc


if __name__ == '__main__':
    train_images, train_labels, test_images, test_labels = get_two_cate()

    print(train_images.shape)
    print(test_images.shape)

    # cv2.imshow('img', train_images[100].reshape(28, -1))
    # cv2.waitKey(0)

    x_train = train_images.astype(np.float64)
    x_test = test_images.astype(np.float64)
    mu = np.mean(x_train, axis=0)
    var = np.var(x_train, axis=0)
    eps = 1e-8
    x_train = (x_train - mu) / np.sqrt(np.maximum(var, eps))
    x_test = (x_test - mu) / np.sqrt(np.maximum(var, eps))

    classifier = LogisticClassifier()
    classifier.train(x_train, train_labels)
    res_labels, scores = classifier.predict(x_test)

    acc = compute_accuracy(test_labels, res_labels)
    print(acc)

    precision, recall, threshold = precision_recall_curve(test_labels, scores, pos_label=1)
    fig = plt.figure()
    plt.plot(precision, recall, label='PR')
    plt.legend()
    plt.show()

    best_th = threshold[np.argmax(precision + recall)]
    print(best_th)
    y_pred = scores > best_th + 0
    acc = compute_accuracy(test_labels, y_pred)
    print(acc)

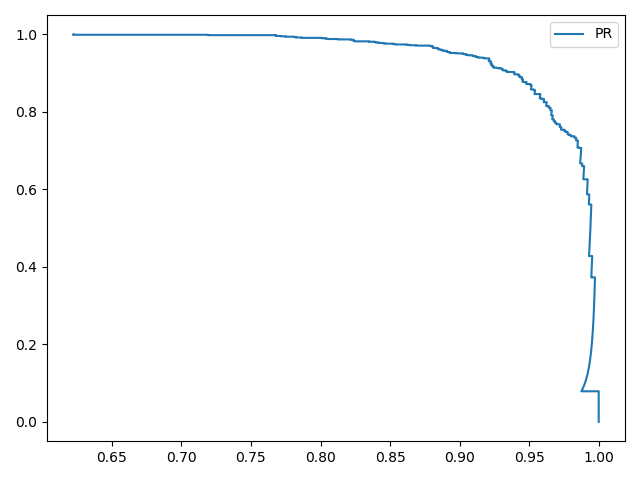
训练结果如下：

1
2
3
4
5
(12000, 784)
(2000, 784)
0.9205                                                 # 阈值为0.5
0.45903893031121357
0.9285                                                 # 阈值为0.4590

通过寻找最佳阈值，使得最后的准确率增加了0.8%

测试2

1
train_images, train_labels, test_images, test_labels = get_two_cate(ratio=1.0 / 6)

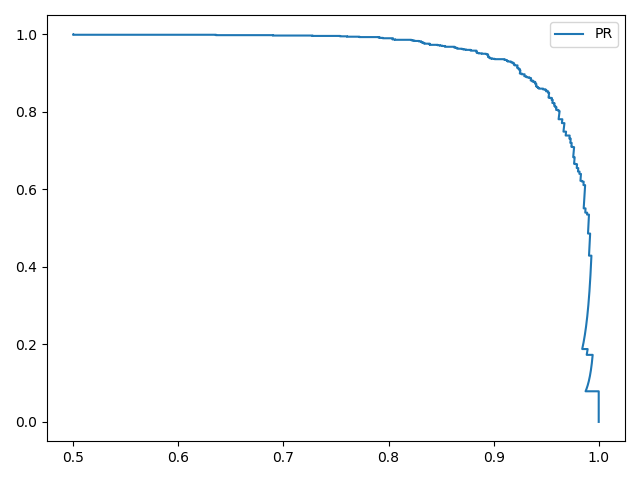
训练结果如下：

1
2
3
4
5
(7000, 784)
(2000, 784)
0.871                                               # 阈值为0.5
0.33526167648147953
0.9215                                            # 阈值为0.3353

从结果可知，PR曲线同样能够在类别数目不平衡的情况下有效的评估分类器性能

相关阅读