Lossless CNN Channel Pruning via Decoupling Remembering and Forgetting

发表于 更新于 分类于
本文字数： 7.2k 阅读时长 ≈ 13 分钟

原文地址：Lossless CNN Channel Pruning via Decoupling Remembering and Forgetting

官方实现：DingXiaoH/ResRep

摘要

We propose ResRep, a novel method for lossless channel pruning (a.k.a. filter pruning), which aims to slim down a convolutional neural network (CNN) by reducing the width (number of output channels) of convolutional layers. Inspired by the neurobiology research about the independence of remembering and forgetting, we propose to re-parameterize a CNN into the remembering parts and forgetting parts, where the former learn to maintain the performance and the latter learn for efficiency. By training the re-parameterized model using regular SGD on the former but a novel update rule with penalty gradients on the latter, we realize structured sparsity, enabling us to equivalently convert the re-parameterized model into the original architecture with narrower layers. Such a methodology distinguishes ResRep from the traditional learning-based pruning paradigm that applies a penalty on parameters to produce structured sparsity, which may suppress the parameters essential for the remembering. Our method slims down a standard ResNet-50 with 76.15% accuracy on ImageNet to a narrower one with only 45% FLOPs and no accuracy drop, which is the first to achieve lossless pruning with such a high compression ratio, to the best of our knowledge.

我们提出了ResRep，一种新的无损通道修剪方法(也称为滤波器修剪)，旨在通过减少卷积层的宽度(输出通道的数量)来精简卷积神经网络(CNN)。受关于记忆和遗忘独立性的神经生物学研究的启发，我们提议将CNN重新参数化为记忆部分和遗忘部分，前者学习保持性能，后者学习提高效率。通过在前者上使用常规的SGD训练重新参数化的模型，而在后者上使用带有惩罚梯度的新的更新规则，我们实现了结构化稀疏性，使得我们能够将重新参数化的模型等效地转换成具有更窄层的原始体系结构。这种方法将ResRep与传统的基于学习的剪枝范式区分开来，传统的剪枝范式对参数进行惩罚以产生结构化稀疏性，这可能抑制记忆所必需的参数。据我们所知，我们的方法将标准的ResNet-50在ImageNet上的准确率为76.15%，缩小到只有45%的浮点运算且准确率没有下降，这是第一个实现如此高压缩比的无损修剪。

简介

完美剪枝：经过剪枝训练后，待剪枝的通道能够获得足够小的值，那么修剪这些通道有可能不会损坏模型性能，能够得到和剪枝前相同的性能

基于训练的剪枝方法评价指标：

  1. Resistance：经过剪枝训练的模型能够和正常训练的模型保持相同的性能，那么称该剪枝方法具有高抗性；
  2. Prunability：如果模型在剪枝阶段拥有高剪枝率，并且仅有些微的性能下降，那么称该剪枝方法具有高剪枝率。

以往基于训练的剪枝方法都存在对高抗性和高剪枝率的平衡，论文提出一种新的剪枝方法 - ResRep。其包含两个关键组件：卷积重参数化（convolutional re-parameterization）以及梯度重置（gradient resetting）

ResRep的灵感来自记忆和遗忘的神经生物学研究。一方面，记忆需要大脑加强一些突触，但削弱其他突触，这类似于CNN的训练过程，使一些参数变大，一些变小。另一方面，通过 spines收缩或缺失来消除突触是经典的遗忘机制之一[50]，是提高生物神经网络能量和空间效率的关键过程，类似于剪枝过程。神经生物学研究表明，记忆和遗忘分别由Rutabaga腺苷酸环化酶介导的记忆形成机制和Rac-regulated spine收缩机制独立控制[11，15，53]，表明通过两个解耦模块控制学习和修剪更合理。

受这种独立性的启发，我们建议将传统范式中耦合的“记忆”和“遗忘”解耦，因为“记忆”(目标函数)和“遗忘”(惩罚损失)都涉及conv参数，以便它们实现权衡。即传统方法强制每个频道“忘记”，去掉“忘记最多”的频道。相反，我们首先将原始模型重新参数化为“记忆部分”和“遗忘部分”，然后将“记忆学习”(即具有原始目标函数的常规SGD)应用于前者以保持“记忆”(原始性能)，并将“遗忘学习”(一种称为梯度重置的定制更新规则)应用于后者以“消除突触”(零输出通道)。更具体地说，我们通过conv-BN-compressor重新参数化原始conv-BN(conv层的缩写，随后是批量归一化[25])序列，其中compressor是逐点(1 × 1) conv层。在训练过程中，我们只给压实机添加惩罚梯度，选择一些压实机通道，并从目标函数中消除它们的梯度。这样的训练过程使得压实机的一些通道非常接近于零，去掉这些通道不会造成修剪造成的伤害。然后我们通过一系列的线性变换，将conv-贝叶斯网络-压缩器序列等效地转换成具有较少通道的单个conv层。最终，生成的模型将具有与原始模型相同的体系结构，但层更窄。图1。b举例说明。请注意，ResRep也可以用于修剪完全连接的层，因为它们相当于1 × 1卷积[40]。

流程

  • 给定一个训练好的模型\(W\)；
  • 执行卷积参数化操作（Convolutional Re-parameterized），在conv-bn层之后添加compactor层，构造新的模型\(\hat{W}\)
    • 初始化compactor权重参数为单位矩阵；
    • 其余部分使用已训练的参数；
  • 开始迭代
    • 输入批量图像，使用正常训练的目标函数计算损失，并求导出梯度；
    • 在compactor层上额外应用梯度重置操作（Gradient Resetting）；
    • 更新梯度
  • 完成训练后，对\(\hat{W}\)中各个compactor层进行滤波器剪枝操作，删除接近于\(0\)的滤波器维度（比如\(norm\leq 10^{-5}\)）
  • 完成剪枝后，将\(\hat{W}\)中conv-bn-compactor融合在一起，得到模型\({W}'\)

基本公式

论文介绍了进行卷积操作和通道剪枝的基本操作。假定卷积层参数如下：

  • 输出通道数：\(D\)
  • 输入通道数：\(C\)
  • 卷积核大小：\(K\times K\)
  • 权重矩阵：\(K=R^{D\times C\times K\times K}\)
  • 偏置：\(b\in R^{D}\)

卷积操作如下：

\[ O = I\circledast K + B(b) \]

  • \(O\)表示输出张量，大小为\(R^{N\times D\times {H}'\times {W}'}\)
  • \(I\)表示输入张量，大小为\(R^{N\times C\times H\times W}\)
  • \(B\)表示广播函数，将偏置\(b\)扩展到\(N\times D\times {H}'\times {W}'\)

如果在卷积层之后添加一个批量归一化层，那么不再需要卷积层的偏置参数，操作如下：

\[ O_{:,j,:,:} = ((I\circledast K)_{:,j,:,:} - \mu_{j})\frac{\gamma_{j}}{\sigma_{j}} + \beta_{j}, \forall 1\leq j\leq D \]

  • \(\mu\)表示归一化层均值；
  • \(\sigma\)表示归一化层标准差；
  • \(\gamma\)表示归一化层缩放因子；
  • \(\beta\)表示归一化层偏置；

假定卷积层下标为\(i\)，经过剪枝后将通道集\(P^{(i)}\subset \{1,2,...,D\}\)移除，剩余通道集为\(S^{(i)}=\{1,2,...,D\}\setminus P^{(i)}\)

经过剪枝后，通道集合\(S^{(i)}\)就是第\(i\)个卷积层的输出通道和第\(i+1\)个卷积层的输入通道

\[ K^{(i)}{}' = K^{(i)}_{S^{(i)},:,:,:}\ \ K^{(i+1)}{}' = K^{(i+1)}_{:,S^{(i)},:,:} \]

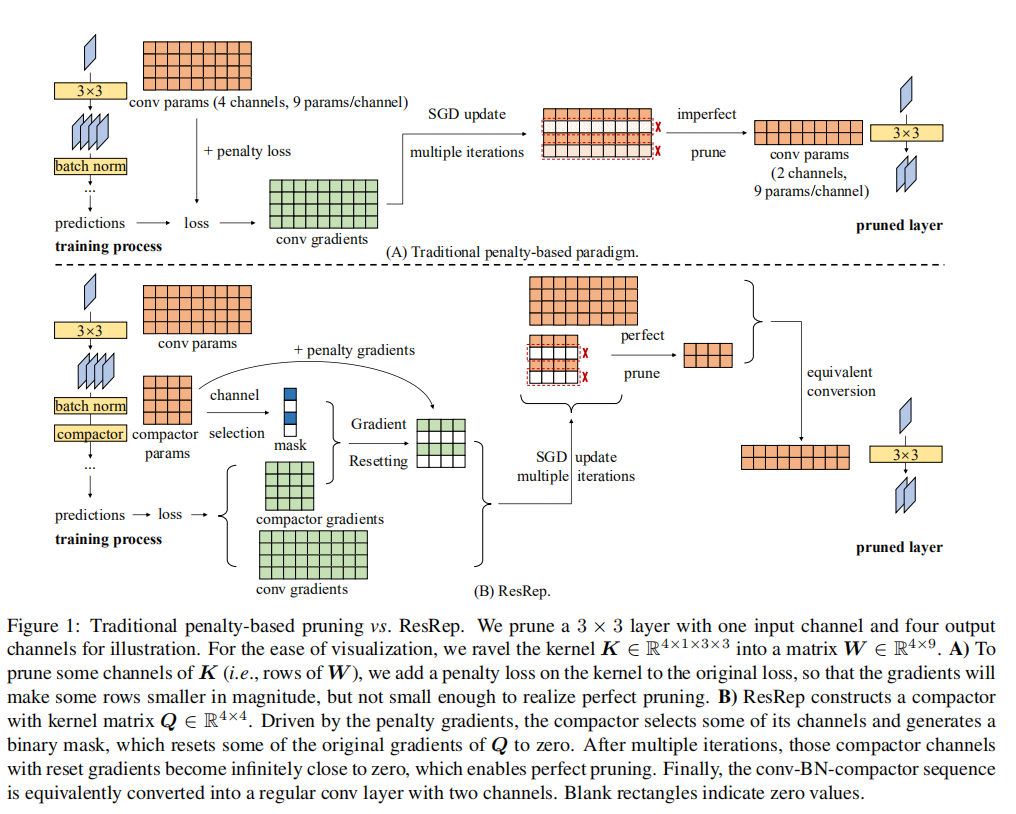
卷积重参数化

卷积重参数化操作分为三部分：

  1. 训练阶段：将模型各个模块显式的区分为记忆部分和遗忘部分，具体实现方式就是在每个Conv-BN层之后额外添加一个Compactor层。Compactor层是一个逐点卷积，其卷积核大小为\(D\times D\)；
  2. 剪枝阶段：仅对Compactor层进行剪枝；
  3. 部署阶段：将每组Conv-BN-Compactor层转换成为单个Conv，最终模型不改变原始模型架构

训练

  • 给定模型\(W\)，指定想要剪枝的Conv-BN层（论文称之为目标层（target layer））
  • 添加一个Compactor层，格式为Conv-BN-Compactor。其中Compactor层是一个逐点卷积，其内核\(Q\in R^{D\times D}\)
  • 完成转换后得到模型\(\hat{W}\)，其Conv-BN层参数保持不变，另外Compactor层权重参数初始化为单位矩阵。这样模型\(\hat{W}\)的输出和原始模型\(W\)保持一致。

剪枝

完成训练后，仅对Compactor层的滤波器维度进行剪枝，其剪枝原则为减去范数大小小于阈值\(\epsilon\)的滤波器通道。具体地说，假设\(P=\{j| \left \| Q_{j,:} \right \|_{2} < \epsilon\}\)为剪去的通道集，\(S = \{ j| \left \| Q_{j,:} \right \|_{2} \ge \epsilon \}\)为剩余的通道集。完成剪枝后，Compactor层的权重大小为\(Q' = Q_{S,:}\)

论文推荐剪枝阈值\(\epsilon = 1\times 10^{-5}\)

完成剪枝后，Compactor层卷积核大小为\(Q'\in R^{D'\times D}\)，以及\(D' = \left | S \right |\)

部署

部署阶段，将Conv-BN-Compactor转换成单个卷积层，其大小为\(K'\in R^{D'\times C\times K\times K}\)，偏置大小为\({b}'\in R^{D'}\)

首先将Conv-BN转换成单个卷积层，其实现如下：

\[ \bar{K}_{j,:,:,:} = \frac{\gamma_{j}}{\sigma_{j}}K_{j,:,:,:}, \ \ \bar{b}_{j} = -\mu_{j}\frac{\gamma_{j}}{\sigma_{j}} + \beta_{j}, \forall 1\leq j\leq D \]

  • \(\bar{K}\)和\(\bar{b}\)是新的卷积层的卷积核以及偏置

接下来就是将Conv-Compactor转换成单个卷积层，其实现如下：

\[ (I\circledast \bar{K} + B(\bar{b}))\circledast {Q}' = I\circledast {K}' + B({b}') \]

卷积操作具有可加性，将上述公式推理如下：

\[ I\circledast \bar{K}\circledast {Q}' + B(\bar{b})\circledast {Q}' = I\circledast {K}' + B({b}') \]

梯度重置

公式

梯度重置的核心在于对遗忘模块进行逐步掩码训练，这样即保证了记忆模块能够很好的进行性能训练，也能够保证模型具有足够的稀疏性。

传统的剪枝训练方式是额外添加一个稀疏损失\(P(K)\)，并设置一个超参数\(\lambda\)控制稀疏训练的强度

\[ L_{total}(X, Y, \Theta ) = L_{pref}(X, Y, \Theta) + \lambda P(K) \]

  • \(X\)表示输入数据
  • \(Y\)表示输入标签
  • \(\Theta\)表示模型参数集
  • \(P(K)\)表示稀疏损失
  • \(K\)表示通道集
  • \(\lambda\)表示稀疏强度

常用的\(P\)包括\(L1/L2\)以及Group Lasso操作（更适用于通道剪枝）。论文使用Group Lasso作为稀疏损失计算函数，其公式如下：

\[ P_{Lasso}(K) = \sum_{j=1}^{D}\left \| F^{(j)} \right \|_{E} \]

  • \(F^{(j)}\)是\(K\)中一组特定的通道（或者称之为待剪枝的通道）
  • \(\left \| F^{(j)} \right \|_{E}\)表示欧式距离，其实现如下

\[ \left \| F \right \|_{E} = \sqrt{\sum_{c=1}^{C}\sum_{p=1}^{K}\sum_{q=1}^{K}F_{c,p,q}^{2}} \]

计算得到的梯度如下：

\[ G(F) = \frac{\partial L_{total}(X, Y, \Theta)}{\partial F} = \frac{\partial L_{pref}(X, Y, \Theta)}{\partial F} + \lambda\frac{F}{\left \| F \right \|_{E}} \]

论文也分析了这种梯度更新方式的缺陷，主要在于目标函数和稀疏函数之间会相互竞争，稀疏函数的目的在于将通道的大小趋向于0，而如果目标函数认为该通道有作用，那么它会放大该通道的大小，论文称这种方式是基于竞争的重要性评估（competence-based importance evaluation）。这种方式会带来两个问题：

  1. 目标函数和稀疏函数共同作用，有可能会偏移模型最优化方向，降低模型性能；
  2. 如果减少了稀疏化强度，那么会导致剪枝率的下降。

基于上面的考虑，论文提出的梯度重置操作如下：

\[ G(F) = \frac{\partial L_{pref}(X, Y, \Theta)}{\partial F}m + \lambda\frac{F}{\left \| F \right \|_{E}} \]

  • \(m\)是一个二值掩码\(m\in \{0, 1\}\)，控制是否对某些通道执行梯度更新

梯度重置操作如下：

  1. 对每个通道都执行梯度更新，但是给予很小的稀疏化强度（\(\lambda=10^{-4}\)），这种小的优化不改变模型性能；
  2. 对于待剪枝的通道（也就是Compactor层），可选的设置\(m=0\)，这样可以保证\(F\)大小稳定的趋向于\(0\)

实现

论文并没有在训练过程中取消对所有Compactor层的目标函数相关的梯度更新，而是设计了一个更新策略：

  1. 假定\(Q\)表示Compactor层的卷积核；
  2. 最开始训练的时候不设置\(m\)的大小为\(0\)；
  3. 经过几轮训练后，\(\left \| Q_{j,:} \right \|\)能够反映第\(j\)个滤波器的重要性。然后开始进行通道选择（channel selection）
    1. 假定模型共有\(n\)个Compactor；
    2. \(m^{(i)}\)表示第\(i\)个Compactor的掩码，是一个大小为\(D^{(i)}\)的二值向量；
    3. 定义\(t^{(i)}\in R^{D^{(i)}}\)是测量向量，其计算公式如下： \[ t^{(i)}_{j} = \left \| Q_{j,:}^{(i)} \right \|_{2}, \forall 1\le j\le D^{(i)} \]
    4. 在每次通道选择过程中，计算\(n\)个Compactor的\(D\)个通道的度量值，进行从小到大排序，每次选择值最小的通道，设置其掩码为\(m_{j}^{(i)}=0\)，其余未选中的通道掩码为\(1\)
    5. 设置超参数\(\theta\)，称之为通道选择限制（channel selection limit），表示通道选择的最大个数。每轮选择一个通道，设置其掩码值为0,，掩码为0的通道数达到\(\theta\)后不再进行选择；
    6. 经过几轮的训练之后，重新设置\(\theta\)值，增加其大小，同时重新开始选择通道（所有掩码初始化为1）

实验

  • 设置稀疏化强度\(\lambda=1e^{-4}\)；
  • 设置初始通道选择限制\(\theta=4\)，每隔200轮\(\theta = \theta + 4\)

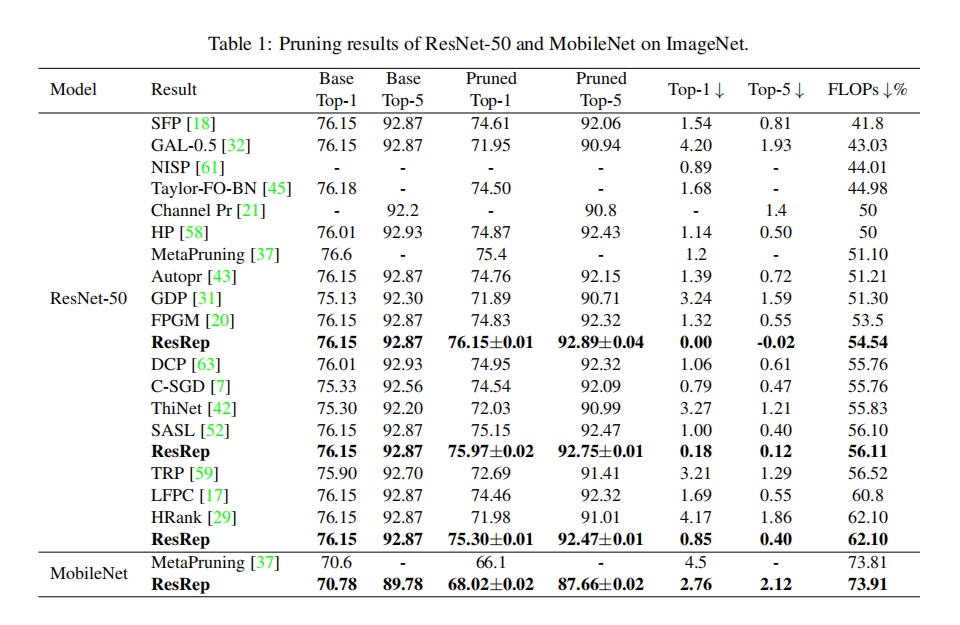
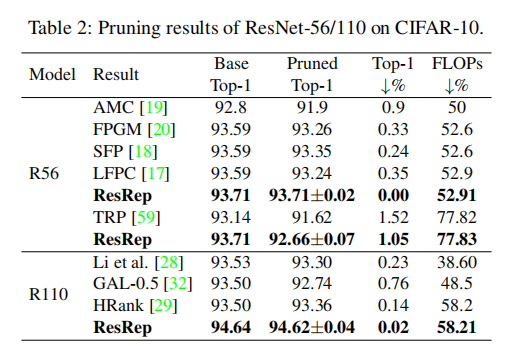
研究

论文研究了分离Res和Rep操作的剪枝操作，其结果如下：

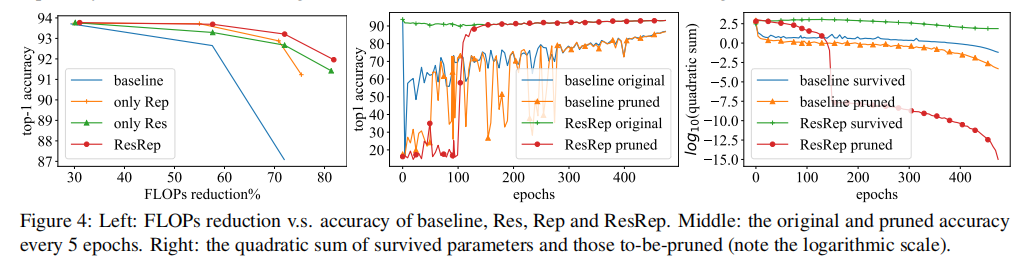
小结

相对于之前的通道剪枝算法，ResRep的理论性更强，通过观察神经学研究，通过梯度重置分离性能训练和稀疏训练，并且通过重参数操作确保训练前后模型架构的一致性

相关阅读