随机失活

发表于 更新于 分类于 ， ， ， ， ， 阅读次数： 本文字数： 2.6k 阅读时长 ≈ 10 分钟

使用前馈神经网络进行检测，测试集的检测率总是低于训练集，尤其是训练集数量不大的情况下，原因在于神经网络在训练过程中不断调整参数以拟合训练数据，在此过程中也学习了训练集噪声，导致泛化能力减弱

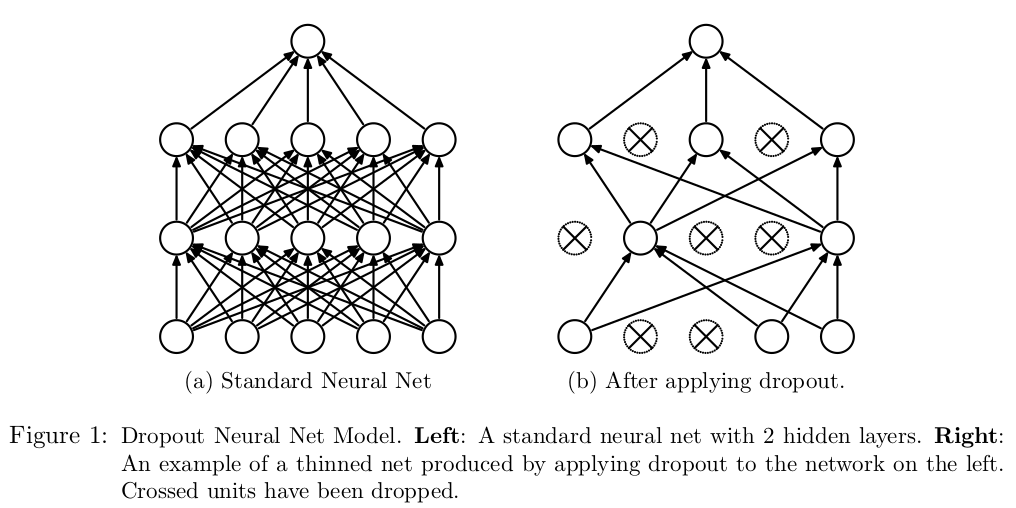
随时失活（dropout）是一种正则化方法，其动机来自于进化中的性别作用理论（a theory of the role of sex in evolution），它通过训练多个不同网络模型，模拟模型组合的方式来提高网络性能，防止网络过拟合

主要内容如下：

  1. 基础知识 - 伯努利分布/均匀分布
  2. 实现原理
  3. 模型描述及改进
  4. 3层神经网络测试

伯努利分布/均匀分布

伯努利分布

伯努利分布（Bernoulli distribution）是离散随机变量分布，如果随机变量只取0和1两个值，并且相应的概率为

则称随机变量服从参数为的伯努利分布

均匀分布

均匀分布（Uniform distribution）也称为矩形分布，它是对称分布，在相同长度间隔的分布概率是等可能的。均匀分布由两个参数和定义，分别表示数轴上的最小值和最大值，缩写为

numpy实现

失活掩模实现：先创建均匀分布在[0,1)中的数组，再比较忽略概率得到失火掩模

函数numpy.random.ranf和numpy.random.rand都实现了[0,1)之间均匀分布，区别在于ranf输入维数元组，rand分别输入每个维数大小

1
2
3
4
5
6
7
8
9
10
11
12
# [0,1)之间的均匀分布实现
>>> size = (2,4)
>>> a = np.random.ranf(size)
>>> a
array([[0.55782603, 0.3881068 , 0.30671933, 0.5932138 ],
       [0.68501697, 0.31336583, 0.79142952, 0.09579494]])
# 伯努利掩模实现
>>> p = 0.5
>>> b = a < p
>>> b
array([[False,  True,  True, False],
       [False,  True, False,  True]])

实现原理

随机失活目的在于避免神经元之间的共适应性（co-adaptation），它鼓励每个隐藏单元在学习有用功能时不依赖于特定的其他隐藏单元来纠正错误

另一种解释是随机失活过程相当于多网络之间的模型平均（modeling averaging with neural networks）。通过模型集成方式，用多个不同网络进行预测，再通过平均预测结果能够有效减少测试集误差率。理论上个隐藏层神经元可组成个稀疏网络，随机失活在每次训练过程中随机忽略隐藏层的神经元（忽略概率是一个超参数），相当于每次训练不同的神经网络

这些神经网络在同一个神经元上共享权重，最后在测试阶段，不再进行随机失活操作，使用神经网络所有隐藏神经元进行计算，但需要对权重乘以概率，以此来平衡平均网络（mean network）多倍于随机失活网络（dropout network）的激活单元

注意一：通常设置隐藏层随机忽略概率为0.5

注意二：论文中还提到输入层神经元也可进行随机失活，其概率通常接近1，比如设置概率为0.9

注意三：多次实验发现输入层神经元失活极易出现损失无法收敛问题

模型描述及改进

原始模型描述及实现

计算符号参考网络符号定义，标准神经网络的前向计算过程如下：

使用随机失活操作后，其前向计算如下：

注意：前向传播过程中失活的神经元在反向传播中其对应梯度为0

numpy实现

对3层神经网络进行随机失活操作如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
class ThreeNet(object):

    def __init__(self, D_in, D_h1, D_h2, D_out, p_h=1.0):
        ...
        self.p_h = p_h

    def forward(self, inputs):
        """
        前向计算，计算评分函数值
        """
        self.N = inputs.shape[0]
        self.a0 = inputs

        self.z1 = inputs.dot(self.w) + self.b
        self.a1 = np.maximum(0, self.z1)
        # 创建失活掩模
        U1 = np.random.ranf(self.a1.shape) < self.p_h
        self.a1 *= U1

        self.z2 = self.a1.dot(self.w2) + self.b2
        self.a2 = np.maximum(0, self.z2)
        # 创建失活掩模
        U2 = np.random.ranf(self.a2.shape) < self.p_h
        self.a2 *= U2

        self.z3 = self.a2.dot(self.w3) + self.b3
        expscores = np.exp(self.z3)
        self.h = expscores / np.sum(expscores, axis=1, keepdims=True)
        return self.h

    def backward(self, output):
        """
        反向传播，计算梯度
        """
        delta = self.h
        delta[range(self.N), output] -= 1
        delta /= self.N

        self.dw3 = self.a2.T.dot(delta)
        self.db3 = np.sum(delta, axis=0, keepdims=True)

        da2 = delta.dot(self.w3.T)
        # 失活掩模
        da2 *= self.U2
        dz2 = da2
        dz2[self.z2 < 0] = 0

        self.dw2 = self.a1.T.dot(dz2)
        self.db2 = np.sum(dz2, axis=0, keepdims=True)

        da1 = dz2.dot(self.w2.T)
        # 失活掩模
        da1 *= self.U1
        dz1 = da1
        dz1[self.z1 < 0] = 0

        self.dw = self.a0.T.dot(dz1)
        self.db = np.sum(dz1, axis=0, keepdims=True)

    def update(self, lr=1e-3, reg_rate=0.0):
        ...

    def predict(self, inputs):
        """
        前向计算，计算评分函数值
        """
        z1 = inputs.dot(self.w) + self.b
        # 输出向量乘以忽略概率p
        a1 = np.maximum(0, z1) * self.p_h

        z2 = a1.dot(self.w2) + self.b2
        # 输出向量乘以忽略概率p
        a2 = np.maximum(0, z2) * self.p_h

        z3 = a2.dot(self.w3) + self.b3
        expscores = np.exp(z3)
        self.h = expscores / np.sum(expscores, axis=1, keepdims=True)
        return self.h

改进一：反向失活

原始模型针对前向/后向传播进行了失活掩模操作，对预测阶段隐藏层输出值进行了等比例缩放

实际操作中预测时间越短越好，所以采用反向失活（inverted dropout）策略

假设原先隐藏层输出为，所以在预测阶段需要称以概率，最终值为

在反向失活操作中，将，那么在预测阶段就不需要再乘以概率，在训练阶段就需要修改为

相当于在训练阶段进行数据放大，在预测阶段正常输出即可

模型描述如下：

numpy实现

反向失活操作如下：

1
2
3
4
5
6
7
def dropout(shape, p):
    assert len(shape) == 2
    res = (np.random.ranf(shape) < p) / p

    if np.sum(res) == 0:
        return 1.0 / p
    return res

集成到网络中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
class ThreeNet(object):

    def __init__(self, D_in, D_h1, D_h2, D_out, p_h=1.0):
        ...
        self.p_h = p_h

    def forward(self, inputs):
        """
        前向计算，计算评分函数值
        """
        self.N = inputs.shape[0]
        self.a0 = inputs

        self.z1 = inputs.dot(self.w) + self.b
        self.a1 = np.maximum(0, self.z1)
        # 创建失活掩模
        U1 = (np.random.ranf(self.a1.shape) < self.p_h) / self.p_h
        self.a1 *= U1

        self.z2 = self.a1.dot(self.w2) + self.b2
        self.a2 = np.maximum(0, self.z2)
        # 创建失活掩模
        U2 = (np.random.ranf(self.a2.shape) < self.p_h) / self.p_h
        self.a2 *= U2

        self.z3 = self.a2.dot(self.w3) + self.b3
        expscores = np.exp(self.z3)
        self.h = expscores / np.sum(expscores, axis=1, keepdims=True)
        return self.h

    def backward(self, output):
        """
        反向传播，计算梯度
        """
        delta = self.h
        delta[range(self.N), output] -= 1
        delta /= self.N

        self.dw3 = self.a2.T.dot(delta)
        self.db3 = np.sum(delta, axis=0, keepdims=True)

        da2 = delta.dot(self.w3.T)
        # 失活掩模
        da2 *= self.U2
        dz2 = da2
        dz2[self.z2 < 0] = 0

        self.dw2 = self.a1.T.dot(dz2)
        self.db2 = np.sum(dz2, axis=0, keepdims=True)

        da1 = dz2.dot(self.w2.T)
        # 失活掩模
        da1 *= self.U1
        dz1 = da1
        dz1[self.z1 < 0] = 0

        self.dw = self.a0.T.dot(dz1)
        self.db = np.sum(dz1, axis=0, keepdims=True)

    def update(self, lr=1e-3, reg_rate=0.0):
        ...

    def predict(self, inputs):
        """
        前向计算，计算评分函数值
        """
        z1 = inputs.dot(self.w) + self.b
        a1 = np.maximum(0, z1)

        z2 = a1.dot(self.w2) + self.b2
        a2 = np.maximum(0, z2)

        z3 = a2.dot(self.w3) + self.b3
        expscores = np.exp(z3)
        self.h = expscores / np.sum(expscores, axis=1, keepdims=True)
        return self.h

空间失活

在4-D张量中，相邻的特征可能是强相关的，因此标准失活操作将无法有效地规范网络，空间失活以通道为单位，随机对整个通道（激活图）进行清零

1
2
3
4
5
6
7
8
9
10
11
12
13
>>> m = nn.Dropout2d(p=0.5)
>>> m(torch.arange(16).reshape(1,4,2,2).float())
tensor([[[[ 0.,  2.],
          [ 4.,  6.]],

         [[ 8., 10.],
          [12., 14.]],

         [[ 0.,  0.],
          [ 0.,  0.]],

         [[ 0.,  0.],
          [ 0.,  0.]]]])

numpy实现

1
2
3
4
5
6
7
8
9
10
def dropout2d(shape, p):
    assert len(shape) == 4
    N, C, H, W = shape[:4]
    U = (np.random.rand(N * C, 1) < p) / p
    res = np.ones((N * C, H * W))
    res *= U

    if np.sum(res) == 0:
        return 1.0 / p
    return res.reshape(N, C, H, W)

3层神经网络测试

3层随机失活神经网络实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
class ThreeLayerNet(Net):
    """
    实现3层神经网络
    """

    def __init__(self, num_in, num_h_one, num_h_two, num_out, momentum=0, nesterov=False, p_h=1.0, p_in=1.0):
        super(ThreeLayerNet, self).__init__()
        self.fc1 = FC(num_in, num_h_one, momentum=momentum, nesterov=nesterov)
        self.relu1 = ReLU()
        self.fc2 = FC(num_h_one, num_h_two, momentum=momentum, nesterov=nesterov)
        self.relu2 = ReLU()
        self.fc3 = FC(num_h_two, num_out, momentum=momentum, nesterov=nesterov)

        self.p_h = p_h
        self.p_in = p_in
        self.U1 = None
        self.U2 = None

    def __call__(self, inputs):
        return self.forward(inputs)

    def forward(self, inputs):
        # inputs.shape = [N, D_in]
        assert len(inputs.shape) == 2
        U0 = F.dropout(inputs.shape, self.p_in)
        inputs *= U0

        a1 = self.relu1(self.fc1(inputs))
        self.U1 = F.dropout(a1.shape, self.p_h)
        a1 *= self.U1

        a2 = self.relu2(self.fc2(a1))
        self.U2 = F.dropout(a2.shape, self.p_h)
        a2 *= self.U2

        z3 = self.fc3(a2)

        return z3

    def backward(self, grad_out):
        da2 = self.fc3.backward(grad_out) * self.U2
        dz2 = self.relu2.backward(da2)
        da1 = self.fc2.backward(dz2) * self.U1
        dz1 = self.relu1.backward(da1)
        da0 = self.fc1.backward(dz1)

    def update(self, lr=1e-3, reg=1e-3):
        self.fc3.update(learning_rate=lr, regularization_rate=reg)
        self.fc2.update(learning_rate=lr, regularization_rate=reg)
        self.fc1.update(learning_rate=lr, regularization_rate=reg)

    def predict(self, inputs):
        # inputs.shape = [N, D_in]
        assert len(inputs.shape) == 2
        a1 = self.relu1(self.fc1(inputs))
        a2 = self.relu2(self.fc2(a1))
        z3 = self.fc3(a2)

        return z3

    def get_params(self):
        return {'fc1': self.fc1.get_params(), 'fc2': self.fc2.get_params(), 'fc3': self.fc3.get_params(),
                'p_h': self.p_h, 'p_in': self.p_in}

    def set_params(self, params):
        self.fc1.set_params(params['fc1'])
        self.fc2.set_params(params['fc2'])
        self.fc3.set_params(params['fc3'])
        self.p_h = params.get('p_h', 1.0)
        self.p_in = params.get('p_in', 1.0)

训练细节

利用cifar-10进行测试，原始图像大小为(32, 32, 3)，加载数据实现： PyNet/data/load_cifar_10.py

测试参数如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 迭代次数
epochs = 300
# 批量大小
batch_size = 256
# 输入维数
D = 3072
# 隐藏层大小
H1 = 2000
H2 = 800
# 输出类别
K = 40

# 学习率
lr = 1e-3
# 正则化强度
reg_rate = 1e-3
# 隐藏层失活率
p_h = 0.5

每隔50次迭代学习率下降一半，共下降4次

1
2
if i % 50 == 49 and i < 200:
    lr /= 2

测试代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
...
    for i in range(epochs):
        start = time.time()
        total_loss = 0
        for j in range_list:
            data = x_train[j:j + batch_size]
            labels = y_train[j:j + batch_size]

            scores = net.forward(data)
            loss = criterion.forward(scores, labels)
            total_loss += loss
            dout = criterion.backward()
            net.backward(dout)
            net.update(lr=lr, reg=reg_rate)
        end = time.time()

        avg_loss = total_loss / len(range_list)
        loss_list.append(float('%.4f' % avg_loss))
        print('epoch: %d time: %.2f loss: %.4f' % (i + 1, end - start, avg_loss))

        if i % 10 == 9:
            # 计算训练数据集检测精度
            train_accuracy = compute_accuracy(x_train, y_train, net, batch_size=batch_size)
            train_accuracy_list.append(float('%.4f' % train_accuracy))
            if best_train_accuracy < train_accuracy:
                best_train_accuracy = train_accuracy

                test_accuracy = compute_accuracy(x_test, y_test, net, batch_size=batch_size)
                if best_test_accuracy < test_accuracy:
                    best_test_accuracy = test_accuracy
                    # save_params(net.get_params(), path='./three-nn-dropout-epochs-%d.pkl' % (i + 1))

            print('best train accuracy: %.2f %%   best test accuracy: %.2f %%' % (
                best_train_accuracy * 100, best_test_accuracy * 100))
            print(loss_list)
            print(train_accuracy_list)

        if i % 50 == 49 and收敛 i < 200:
            lr /= 2收敛
...

完整代码地址： PyNet/src/t收敛hree_nn_dropout_cifar_10.py

训练结果

进行2种不同网络测试：

  • 标准神经网络
  • 失活神经网络，隐藏层忽略概率为

训练300次后，最好的训练和测试精度如下：

训练精度 测试精度
A 100% 57.63%
B 99.79% 60.01%

随机失活损失和训练精度如下：

标准3层神经网络损失和训练精度如下：

两者比较如下：

分析

从训练结果可看出失活神经网络比标准神经网络泛化能力更强

从图中可以看出，失活神经网络比标准神经网络需要更多训练才能收敛

相关阅读