1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
|
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torch.optim.lr_scheduler as lr_scheduler
from torch.utils.data import DataLoader
import torchvision.transforms as transforms
import torchvision.datasets as datasets
import matplotlib.pyplot as plt
import time
batch_size = 256
epochs = 1000
lr = 1e-2
p_h = 0.5
def load_cifar_10_data(batch_size=128, shuffle=False):
data_dir = '/home/lab305/Documents/data/cifar_10/'
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean=(0.5, 0.5, 0.5), std=(0.5, 0.5, 0.5))
])
train_data_set = datasets.CIFAR10(root=data_dir, train=True, download=True, transform=transform)
test_data_set = datasets.CIFAR10(root=data_dir, train=False, download=True, transform=transform)
train_loader = DataLoader(train_data_set, batch_size=batch_size, shuffle=shuffle)
test_loader = DataLoader(test_data_set, batch_size=batch_size, shuffle=shuffle)
return train_loader, test_loader
class LeNet5(nn.Module):
...
...
def compute_accuracy(loader, net, device):
total = 0
correct = 0
for item in loader:
data, labels = item
data = data.to(device)
labels = labels.to(device)
scores = net.predict(data)
predicted = torch.argmax(scores, dim=1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
return correct / total
if __name__ == '__main__':
train_loader, test_loader = load_cifar_10_data(batch_size=batch_size, shuffle=True)
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
net = LeNet5(3, p=p_h).to(device)
criterion = nn.CrossEntropyLoss().to(device)
optimer = optim.SGD(net.parameters(), lr=lr, momentum=0.9)
stepLR = lr_scheduler.StepLR(optimer, step_size=150, gamma=0.5)
best_train_accuracy = 0.99
best_test_accuracy = 0
loss_list = []
train_list = []
for i in range(epochs):
num = 0
total_loss = 0
start = time.time()
net.train()
for j, item in enumerate(train_loader, 0):
data, labels = item
data = data.to(device)
labels = labels.to(device)
scores = net.forward(data)
loss = criterion.forward(scores, labels)
optimer.zero_grad()
loss.backward()
optimer.step()
total_loss += loss.item()
num += 1
end = time.time()
stepLR.step()
avg_loss = total_loss / num
loss_list.append(float('%.4f' % avg_loss))
print('epoch: %d time: %.2f loss: %.4f' % (i + 1, end - start, avg_loss))
if i % 20 == 19:
net.eval()
train_accuracy = compute_accuracy(train_loader, net, device)
train_list.append(float('%.4f' % train_accuracy))
if best_train_accuracy < train_accuracy:
best_train_accuracy = train_accuracy
test_accuracy = compute_accuracy(test_loader, net, device)
if best_test_accuracy < test_accuracy:
best_test_accuracy = test_accuracy
print('best train accuracy: %.2f %% best test accuracy: %.2f %%' % (
best_train_accuracy * 100, best_test_accuracy * 100))
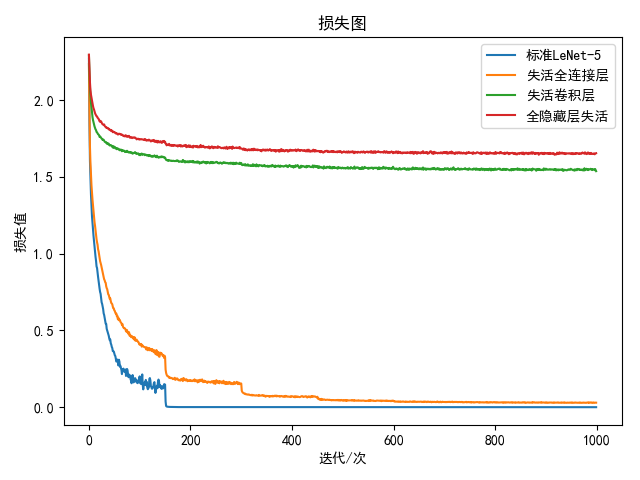
print(loss_list)
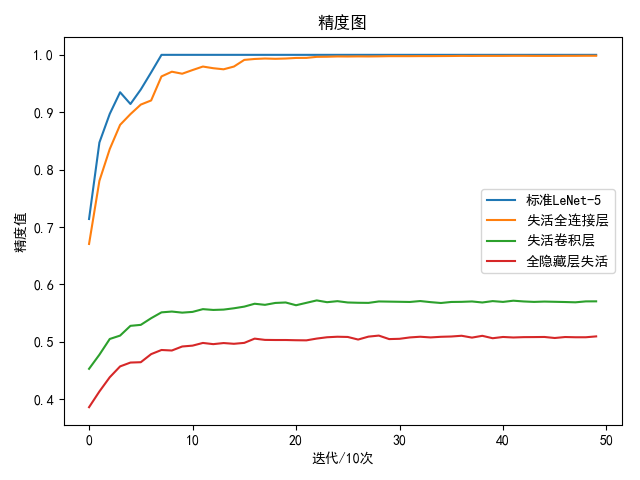
print(train_list)
|
