Paying More Attention to Attention
官方实现:szagoruyko/attention-transfer
摘要
Attention plays a critical role in human visual experience. Furthermore, it has recently been demonstrated that attention can also play an important role in the context of applying artificial neural networks to a variety of tasks from fields such as computer vision and NLP. In this work we show that, by properly defining attention for convolutional neural networks, we can actually use this type of information in order to significantly improve the performance of a student CNN network by forcing it to mimic the attention maps of a powerful teacher network. To that end, we propose several novel methods of transferring attention, showing consistent improvement across a variety of datasets and convolutional neural network architectures. Code and models for our experiments are available at this https URL
注意力在人类视觉体验中起着至关重要的作用。此外,最近已经证明,在将人工神经网络应用于来自诸如计算机视觉和自然语言处理等领域的各种任务的背景下,注意力也可以发挥重要作用。在这项工作中,我们表明,通过适当定义卷积神经网络的注意力,实际上可以使用这种类型的信息,通过迫使学生模拟强大的教师网络的注意力图,来显著提高学生CNN网络的性能。为此,我们提出了几种转移注意力的新方法,在各种数据集和卷积神经网络架构中表现出一致的改进。我们实验的代码和模型开源在https://github.com/szagoruyko/attention-transfer
引言
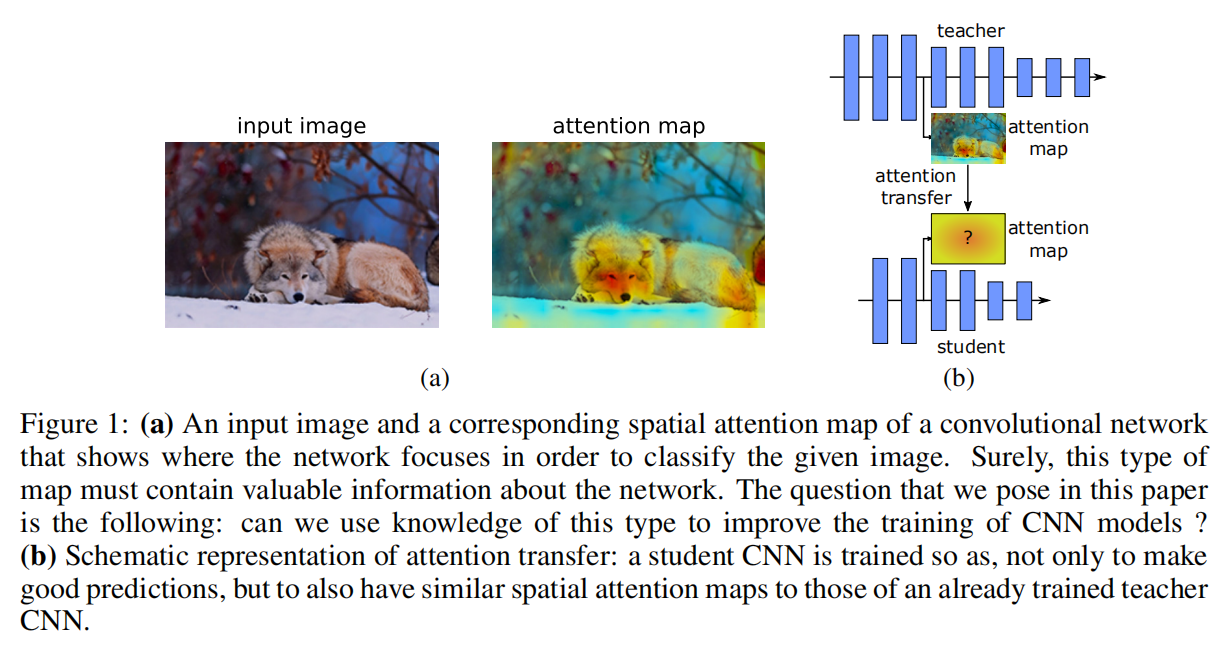
- 提出注意力可以作为知识迁移的一种机制;
- 提出了两种空间注意力图(基于激活和基于梯度)的使用;
- 通过实验(不同数据集、不同深度架构(包括残差以及非残差结构))证明基于注意力的知识迁移方法的有效性;
- 通过实验证明了基于激活的注意力迁移(
activation-based attention transfer)比全激活迁移(full-activation transfer)更有效,并且注意力迁移可以和知识蒸馏方法相结合。
基于激活的注意力迁移
计算公式
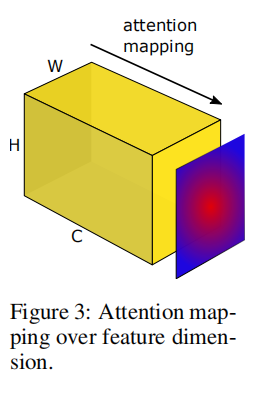
假定单个卷积层输出张量为
论文假定单个隐藏层神经元激活的绝对值可以看成该神经元重要性的评估,所以对于整个输出张量
论文考虑了3种计算方式:
- 计算同一通道维度的神经元激活的绝对值之和:
; - 计算同一通道维度的神经元激活的
次幂之和: ; - 计算同一通道维度的神经元激活的
次幂最大值: ;
其中
其实论文的这种公式编写方式挺奇怪的,反正它的意思就是对输入张量空间维度上每个像素点基于通道维度按照某种方式进行统计,得到一个2D激活图
空间相关性
论文通过比较不同性能的网络架构发现,空间激活图不仅与图像级别上的预测对象具有空间相关性,而且这些相关性在具有更高精度的网络中也往往更高,并且更强的网络在弱网络没有的地方具有注意力峰值。如下图所示

初级/中级/高级特征
另外,论文也发现使用网络不同层计算得到的注意力图,其能够反映不同级别的特征。比如在第一层中,低级特征梯度点的神经元激活值较高;在中间层,眼睛或车轮等最具辨识度的区域的激活值较高;在最后几层,空间特征图能够反映完整的目标。
论文给出一个示例,使用人脸识别网络的中间层得到的注意力图在眼睛、鼻子和嘴唇周围具有更高的激活,并且最高层的空间激活图对应于全脸,如下图所示。

不同
论文论述了不同激活函数计算公式之间的属性差异性:
- 和
相比较, 将更大的权重赋值给拥有更高激活值的空间像素点,也就是更有判别力的区域拥有更大的激活值; - 对于同一个空间像素点,
将通道维度上最大的激活值作为该位置的权重,而 更倾向于通道维度上拥有多个高激活值的空间像素点。
不同的激活函数确实会有差异性,不过最后还是需要通过实验结果进行评判。从后续的试验结果来看,基于
损失函数
论文会采集教师和学生网络的多个层输出张量进行空间注意力图计算。以ResNet为例,教师网络和学生网络拥有相同的网络架构,但是在深度上会有差异性:
- 相同深度:成对计算每个残差块(
residual block)输出的激活图之间的损失; - 不同深度:成对计算每个残差块组(
residual block group)输出的激活图之间的损失。
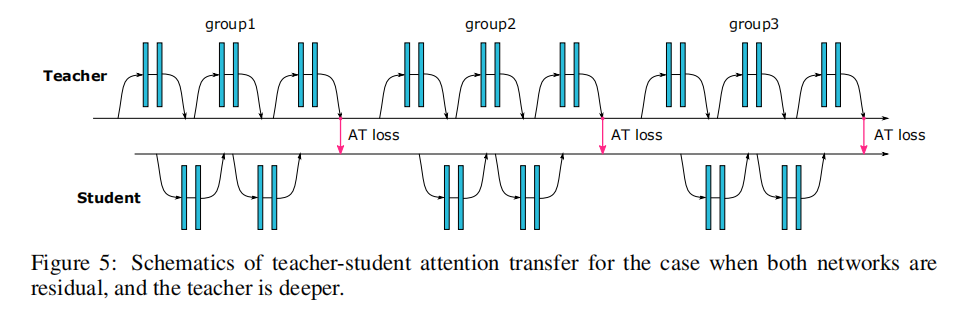
损失函数定义如下:
$$
L_{AT} = L(W_{S}, x) + \frac{\beta}{2}\sum_{j\in I}\left | \frac{Q_{S}^{j}}{\left | Q_{S}^{j} \right |{2}} - \frac{Q{T}^{j}}{\left | Q_{T}^{j} \right |_{2}} \right | _{p}
$$
:学生网络; :教师网络; :学生网络权重集合; :教师网络权重集合; :标准的交叉熵损失; :所有成对的教师-学生激活层下标; 表示以向量形式展示的学生网络第 层的注意力图; 表示以向量形式展示的教师网络第 层的注意力图; 表示范数类型。在论文中使用 。
注意一:论文特别强调了对于注意力图的归一化操作
注意二:在上述的表达式中,假定了成对计算的学生网络-教师网络输出的注意力图拥有相同的空间分辨率。实际操作过程中,如果不匹配的话,需要额外添加一个转换层保证两者拥有相同的分辨率大小
注意三:在上述损失函数描述中,还可以额外添加KD损失,在后续实验中也发现了添加KD损失能够提升学生网络性能
基于梯度的注意力迁移
使用梯度作为注意力图输入,可以看成输入数据的敏感性图(an input sensitivity map),即注意力图的某个位置大小可以看成网络对于输入数据中该位置的关注程度。比如,输入图片中该像素点强度有了很小的变化,但是在网络输出中产生了很大的变化,那么可以判定网络特别关注于该位置的变化。
首先定义学生/教师网络中相对于输入的梯度计算公式
其损失函数计算如下:
其中
总的来说,论文写的有点绕,其实现流程应该如下
- 单独计算学生网络和教师网络的损失函数;
- 然后单独计算学生网络和教师网络对应于输入数据
的梯度 和 ; - 最后计算学生网络基于
的梯度,进行反向传播更新梯度。
为了进一步提高学生网络的水平翻转不变性,论文还提出保持教师网络输入数据不变,水平翻转学生网络的输入数据进行训练,通过后续实验也证明了这种方式能够提高模型泛化能力
在后续的实验中可以发现,论文还是更倾向于基于激活的注意力迁移方式
实验
在CIFAR数据集中同时实验了基于激活和基于梯度的注意力迁移算法;在更大的数据集(CUB/Scenes/ImageNet)上实验了基于激活的注意力迁移算法。
CIFAR10
基于激活的注意力迁移
在CIFAR10数据集上实验了拥有相同深度的网络架构(WRN-16-2/WRN-16-1),以及不同深度的网络架构(WRN-40-1/WRN-16-1, WRN-40-2/WRN-16-2)。其结果如下图所示,AT均实现了显著的提高,同时AT+KD实现了最好的效果。
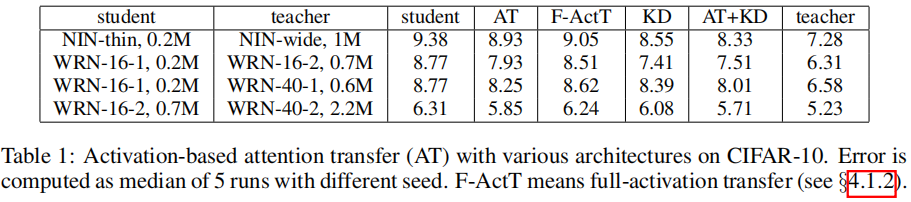
论文同时研究了是否学生-教师网络的每对激活图损失均提供了重要的信息,以WRN为例,分别训练仅包含group1/group2/group3输出的成对激活图损失,其训练结果为8.11、7.96、7.97,而添加每对损失同时进行训练的结果是7.93。所以每个损失都会带来额外的注意力转移信息。
论文也比较了不同
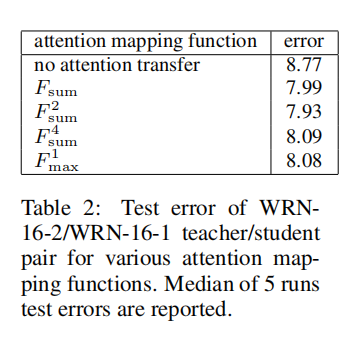
- 基于
- 基于
在后续实验中,论文采用了
AT vs. Full Activation
论文对AT和全激活(使用整个输出3D张量进行注意力图计算)训练进行了比较,不再详细描述,反正就是AT好
基于梯度的注意力迁移
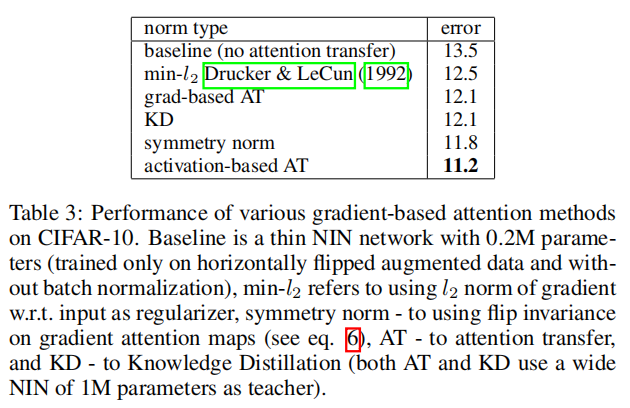
Sences/CUB
论文挑选了两个大数据集进行实验:
Caltech-UCSD Birds-200-2011 fine-grained classification (CUB)MIT indoor scene classification (Scenes)
使用ResNet-34和ResNet-18作为教师-学生网络,它们首先在ImageNet上进行训练,然后在两个数据集上进行微调。首先对ResNet-34进行微调训练,完成后对ResNet-18进行AT/KD训练

使用group执行注意力图计算。
从实验结果来看,AT和KD训练均实现了性能提高,尤其在细粒度数据集上,AT表现出更好的效果,说明了对于细粒度识别而言中间层注意力的重要性。
ImageNet
在ImageNet数据集上,使用ResNet-34和ResNet-18作为教师-学生网络。使用group执行注意力图计算。
从实验结果来看,AT实现了性能提升,如下图所示。
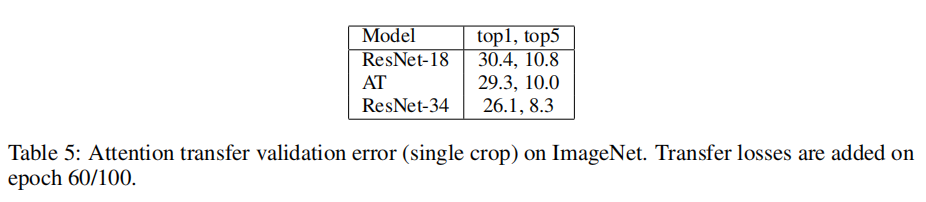
对于KD,论文并没有给出实验记录,不过从它的描述来看,KD训练的要求很高,需要相同架构的学生-教师网络才能够更快的收敛以及得到很好的性能提升。
小结
- 论文提出了基于注意力的知识迁移实现,通过迁移教师网络中间层输出特征的注意力图,能够帮助学生网络得到更好的泛化性能。
- 论文提出了两种注意力图计算方式,分别是基于激活和基于特征的注意力图计算;
- 从实验结果来看,基于激活的注意力迁移算法实现了最好的性能提升。
进一步探索方向:总的来说,就是更丰富的实验,结合其他知识迁移算法
AT+KD;AT+Hints;AT+Hints+KD;