FitNets: Hints for Thin Deep Nets

发表于 更新于 分类于
本文字数： 4.9k 阅读时长 ≈ 9 分钟

原文地址：FitNets: Hints for Thin Deep Nets

官方实现：adri-romsor/FitNets

摘要

While depth tends to improve network performances, it also makes gradient-based training more difficult since deeper networks tend to be more non-linear. The recently proposed knowledge distillation approach is aimed at obtaining small and fast-to-execute models, and it has shown that a student network could imitate the soft output of a larger teacher network or ensemble of networks. In this paper, we extend this idea to allow the training of a student that is deeper and thinner than the teacher, using not only the outputs but also the intermediate representations learned by the teacher as hints to improve the training process and final performance of the student. Because the student intermediate hidden layer will generally be smaller than the teacher's intermediate hidden layer, additional parameters are introduced to map the student hidden layer to the prediction of the teacher hidden layer. This allows one to train deeper students that can generalize better or run faster, a trade-off that is controlled by the chosen student capacity. For example, on CIFAR-10, a deep student network with almost 10.4 times less parameters outperforms a larger, state-of-the-art teacher network.

虽然深度有助于提高网络性能，但它也会使基于梯度的训练变得更加困难，因为深度网络往往更具非线性。最近提出的知识蒸馏方法旨在获得小型且快速执行的模型，它表明学生网络可以模仿大型教师网络或网络集合的软输出。在本文中，我们扩展了这一理念，允许比教师网络更深、更小的学生网络进行训练，不仅仅使用了教师网络输出，还使用教师网络学习到的中间表示作为提示，以改进训练过程和学生的最终表现。由于学生网络的中间隐藏层通常比教师网络的中间隐藏层小，因此引入了附加参数以将学生隐藏层映射到教师隐藏层的预测。这使我们能够训练更深的学生网络，通过设计学生网络，可以使他们能够拥有更好的性能或者能够运行更快。例如，在CIFAR-10上，参数少近10.4倍的深度学生网络比更大、最先进的教师网络表现更好。

引言

论文分析了之前有关模型压缩的方法，发现之前的方法均关注于如何压缩教师模型或者多个模型集成到一个类似宽度/深度或者更窄宽度/深度的学生网络中，而作者通过对深度网络的研究，提出网络深度的重要性，设计了一个窄而深（相对于教师网络）的学生网络（FitNets），并且基于KD（知识蒸馏）的实现，额外利用了中间隐藏层的特征（称之为intermediate-level hints），指导学生网络进行训练。

KD

论文首先描述了KD（知识蒸馏）提出的学生-教师训练框架。首先定义教师网络：

  1. \(T\)：教师网络；
  2. \(a_{T}\)：logits；
    1. 如果教师网络仅存在一个，那么\(a_{T}\)就是教师网络最后的输出向量；
    2. 如果教师网络是多个模型集成，那么\(a_{T}\)就是多个网络输出向量的算术或者几何平均；
  3. \(P_{T}\)：probs，logits经过softmax层得到的分类概率；

对于教师网络而言，其输出和概率计算如下：

\[ P_{T} = softmax(a_{T}) \]

同理，定义学生网络如下：

  1. \(S\)：学生网络；
  2. \(a_{S}\)：logits，学生网络最后的输出向量；
  3. \(P_{S}\)：分类概率。

对于学生网络而言，其输出和概率计算如下：

\[ P_{S} = softmax(a_{S}) \]

另外，对于同一个训练图片而言，学生网络和教师网络拥有相同的真值标签\(y_{true}\)。

在训练学生网络之前先对教师网络进行训练，所以教师网络的输出概率\(P_{T}\)有可能非常接近于样本真值标签的one-hot编码（就是属于真值标签的概率非常高，其余接近于0）。KD提出一个超参数：蒸馏温度\(\tau\)，来平滑教师网络的输出概率，为学生网络的训练提供更多有用的信息。

学生网络的损失函数定义如下：

\[ L_{KD}(W_{S}) = H(y_{true}, P_{S}) + \lambda H(P_{T}^{\tau}, P_{S}^{\tau}) \]

其中

  • \(P_{T}^{\tau} = softmax(\frac{a_{T}}{\tau})\)
  • \(P_{S}^{\tau} = softmax(\frac{a_{S}}{\tau})\)
  • \(H(\cdot)\)指的是交叉熵；
  • \(\lambda\)是超参数，用于平衡两个交叉熵对于训练的影响。

Hint

论文介绍了基于hint的蒸馏训练，hint指的是教师网络中间层的特征，用来指导学生网络的训练。在学生网络中，同样选择一个隐藏层（称之为guided layer，被指导层），对教师网络的hint特征进行学习。guided layer对hint特征进行拟合，这样导致学生网络拥有更少的灵活性，避免网络过拟合。

在论文设置中，将教师网络的Hint设置为中间层输出特征，同样的，设置学生网络的guided layer为中间层。在训练过程中，通常教师网络的hint层输出宽度大于学生网络的guided layer输出，所以额外设置了一个回归器，用于映射两个特征向量。

在基于hint的训练框架中，首先训练学生网络的前半部分（直到guided layer）以及这个回归器，损失函数如下：

\[ L_{HT}(W_{Guided}, W_{r}) = \frac{1}{2} \left \| u_{h}(x; W_{Hint}) - r(v_{g}(x; W_{Guided}); W_{r}) \right \|^{2} \]

  • \(u_{g}\)和\(v_{g}\)分别表示教师/学生网络的前半部分，直到各自的hint层和guided层；\(W_{Hint}\)和\(W_{Guided}\)分别是对应的层参数；
  • \(r\)指的是回归器，作用于学生网络guided层的输出，\(W_{r}\)是对应的参数；

论文在实际操作中发现使用全连接层作为回归器增加了参数数目以及内存占用。假定

  1. \(N_{h,1}\times N_{h, 2}\)以及\(O_{h}\)分别是教师网络hint层的空间大小以及通道数；
  2. \(N_{g,1}\times N_{g, 2}\)以及\(O_{g}\)分别是学生网络guided层的空间大小以及通道数；

如果使用全连接网络回归器，那么其参数数目为

\[ N_{h, 1}\times N_{h, 2}\times O_{h}\times N_{g, 1}\times N_{g, 2}\times O_{g} \]

论文设计了一个卷积层回归器，其输入为学生网络的guided层输出特征，其输出大小与教师网络的hint层输出特征大小一致。

  1. 输入空间大小为\(N_{g, 1}\times N_{g, 2}\)；
  2. 输出空间大小为\(N_{h,1}\times N_{h, 2}\)；
  3. 卷积核大小为\(k_{1}\times k_{2}\)，其符合\(N_{g, i} - k_{i} + 1 = N_{h, i}, i\in \{1, 2\}\)

卷积网络回归器的参数数目为

\[ k_{1}\times k_{2}\times O_{h}\times O_{g} \]

其数目\(k_{1}\times k_{2}\)远小于\(N_{h, 1}\times N_{h, 2}\times N_{g, 1}\times N_{g, 2}\)

训练

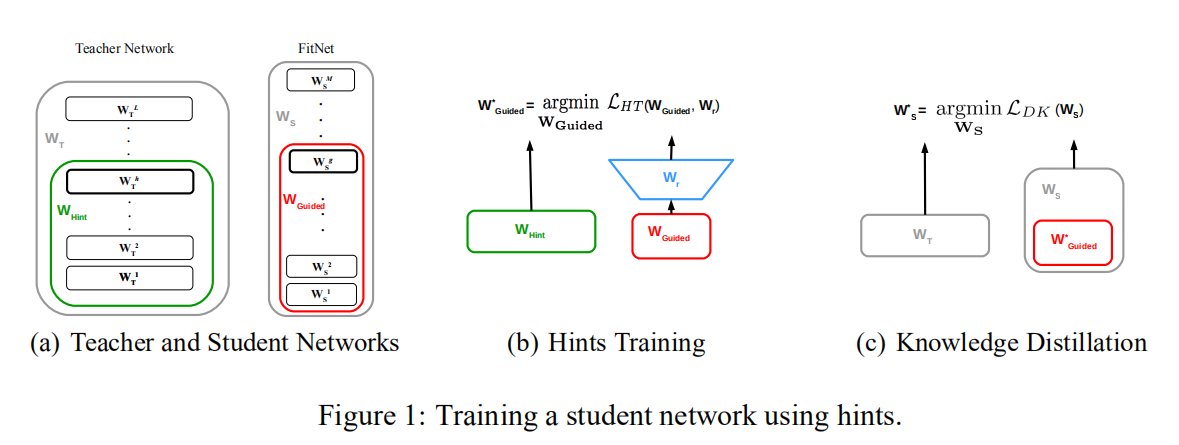
共分为两个阶段训练：

  • 第一阶段：利用教师网络的hint层预训练学生网络的前半部分（直到guided层）和一个卷积网络回归器，如上图（b）所示；
  • 第二阶段：使用第一阶段学生网络训练得到的前半部分参数值作为初始化，然后对整个学生网络进行蒸馏训练。

整体算法描述如下图所示：

FitNets

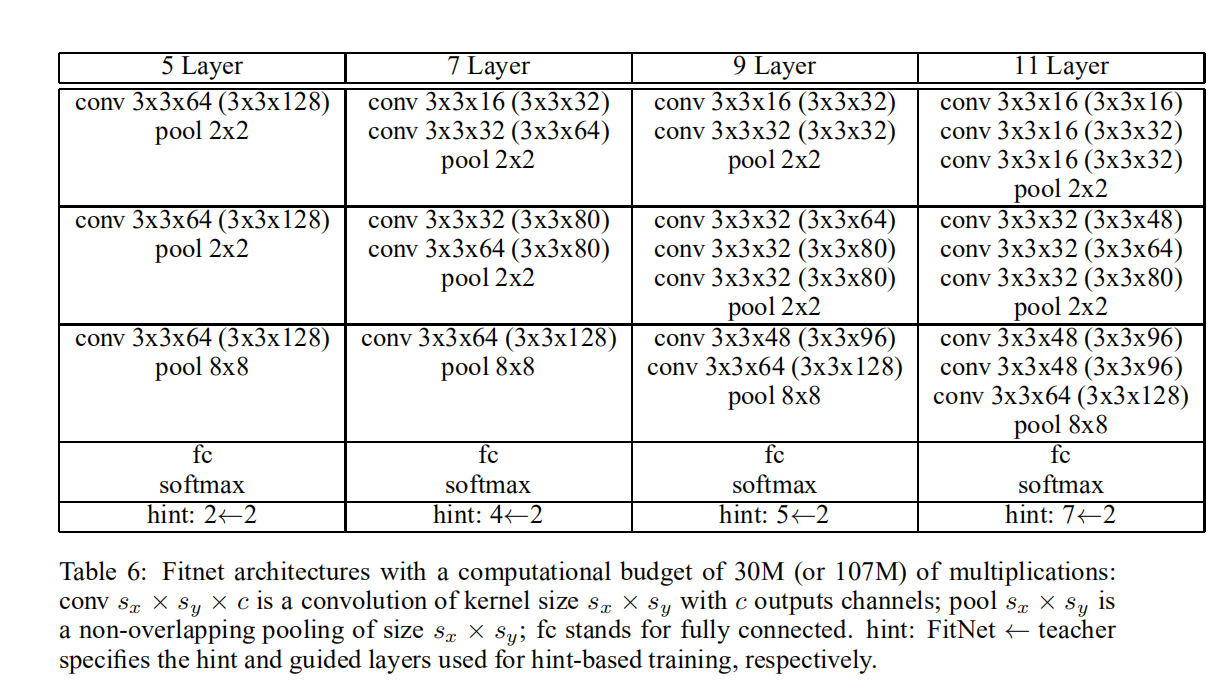
论文在不同数据集下实验了不同计算资源和推理速度的FitNets，完整信息可以查看附录

实验

论文在不同数据集上实验了不同深度的FitNet，表明了基于Hint的训练是有效的，同时也证明了深度属性是很好的提高性能的维度

CIFAR10/CIFAR100

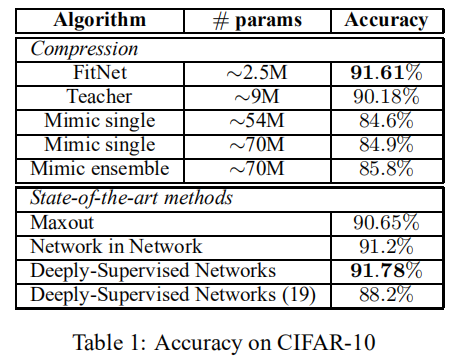
SVHN/MNIST

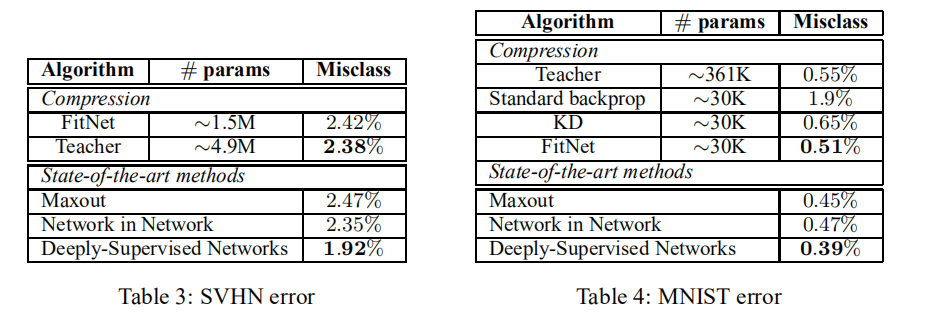
分析

论文在CIFAR10上实验了在给定计算资源（应该指的是Flops）的前提下，不同深度的网络（拥有相同计算资源，通过调节每层宽度来匹配）在不同优化方式（BP vs. KD vs. HT）的表现

BP vs. KD vs. HT

论文设计了两种计算资源：30M和107M乘法运算，以及设计了多种网络架构（层数不一样）。其实验结果如下图所示：

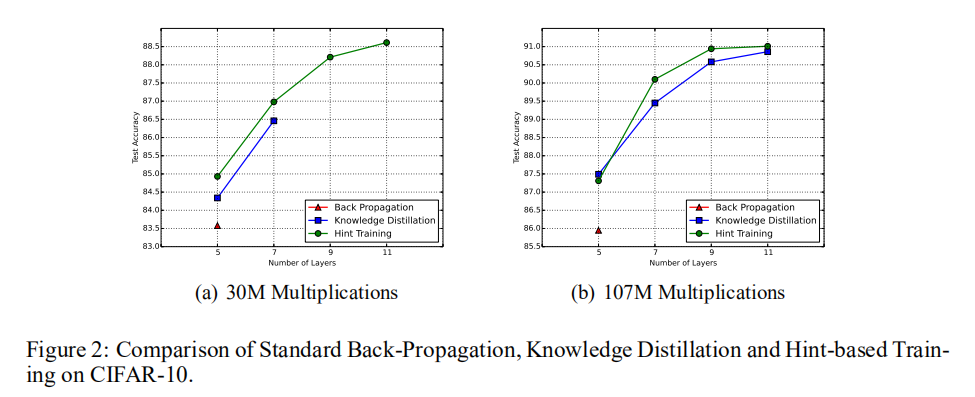
在30M计算资源约束下，

  1. 使用标准的反向传播流程进行训练，最深能够训练5层网络；
  2. 使用KD进行训练，最深能够训练7层网络；
  3. 使用HT进行训练，最深能够训练11层网络

KD和HT惟一差别在于其拥有不同的初始化参数空间，实验结果表明HT可以引导学生在参数空间中找到一个更好的初始位置。

在107M计算资源约束下，

  1. 固定网络架构以及计算资源的情况下，HT能够比另外两种训练方式得到更高的性能；
    1. 论文分析是因为基于HT的预训练能够实现强大的正则化器作用，帮助模型得到更好的泛化性能；
  2. 给定计算资源的情况下，更深的网络能够比更浅的网络得到更高的性能；
    1. 这说明了深度是提高模型性能的重要维度。

通过上述实验，论文得到以下结论：

  1. 使用HT，能够比标准BP以及KD得到更深的模型；
  2. 给定固定计算资源，更深的网络拥有更好的性能。

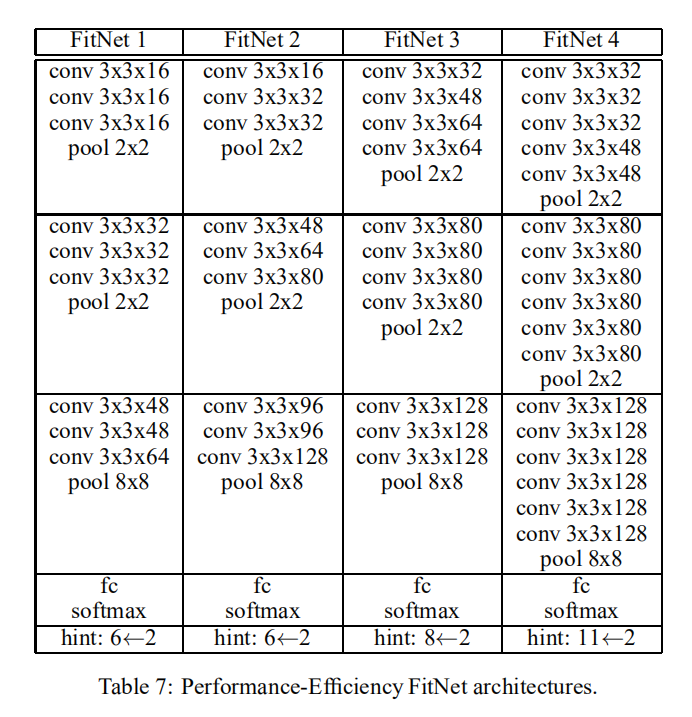
性能 vs. 速度

论文实验了不同架构的FitNet在性能和速度上的比较，证明了论文设计的FitNet架构的有效性。其实验结果如下图所示：

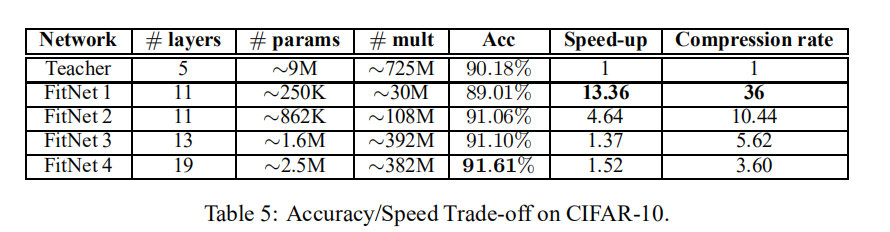
小结

论文主要贡献：

  1. 相同计算资源和网络架构条件下，更深的网络拥有更好的性能；
  2. 在KD训练之前应用HT训练得到前半部分网络的预训练参数，能够作为正则化器作用得到更好的泛化性能；
  3. 应用知识迁移技术的学生网络不需要一定是类似宽度/深度或者更窄宽度/深度的架构，也可以是性能更强大、网络更深的架构；
  4. 论文设计的FitNet网络架构具有极强的性能。

在本文研究期间，最好的深度神经网络还停留在GooLeNet和VGGNet，并不了解之后出现的ResNet等模型能够极大的释放网络深度限制，所以论文特别关注于模型的深度属性。另外，本文首次提出了通过中间层特征（intermediate-level hints）来加速学生模型蒸馏训练，相比于宽且深的教师网络，能够得到窄且更深的学生网络，通过实验证明了其有效性。

进一步探索方向：

  1. 论文并没有给出HT之后进行KD训练的具体参数值（比如蒸馏温度啥的）；
  2. 论文在小数据集上进行了充分实验，但是并没有给出大数据集（比如ImageNet）上的实验报告；
  3. 论文在实验中也描述了不同训练方式（分阶段训练、级联训练、使用不同位置的hint特征等等）对于知识迁移的影响，但是并没有给出实验报告；
  4. 论文所在的时间点并没有出现更丰富的网络架构，目前的网络模型（比如ResNet/MobileNet）已经实现了极深的设计，那么再使用更深的学生网络能够奏效。