MultiGrain: a unified image embedding for classes and instances

发表于 2022-08-06 更新于 2025-12-07 分类于图像检索/image retrieval 阅读次数：本文字数： 3.6k 阅读时长 ≈ 13 分钟

原文地址：MultiGrain: a unified image embedding for classes and instances

摘要

MultiGrain is a network architecture producing compact vector representations that are suited both for image classification and particular object retrieval. It builds on a standard classification trunk. The top of the network produces an embedding containing coarse and fine-grained information, so that images can be recognized based on the object class, particular object, or if they are distorted copies. Our joint training is simple: we minimize a cross-entropy loss for classification and a ranking loss that determines if two images are identical up to data augmentation, with no need for additional labels. A key component of MultiGrain is a pooling layer that takes advantage of high-resolution images with a network trained at a lower resolution.

When fed to a linear classifier, the learned embeddings provide state-of-the-art classification accuracy. For instance, we obtain 79.4% top-1 accuracy with a ResNet-50 learned on Imagenet, which is a +1.8% absolute improvement over the AutoAugment method. When compared with the cosine similarity, the same embeddings perform on par with the state-of-the-art for image retrieval at moderate resolutions.

MultiGrain是一个能够得到紧凑向量的网络架构，同时适用于图像分类和特定目标检索。它基于标准的分类网络架构，在网络顶部生成一个包含粗粒度和细粒度信息的嵌入表示，因此可以用于识别目标类别、特定目标对象或者扭曲图片。联合训练非常简单：不需要额外的标签，最小化用于分类的交叉熵损失以及确定两幅图像在数据扩充后是否一致的排序损失。MultiGrain的关键在于池化层，它在训练时仅需较低的分辨率，而在测试阶段能够利用高分辨率图像获取更好性能。

把学习得到的嵌入表示输入到线性分类器，MultiGrain能够实现最先进的分类精度。基于ImageNet学习的ResNet-50获得79.4%的top-1精度，这比AutoAugment方法获取的精度绝对值提高了+1.8%。基于余弦相似度进行检索时，在中等分辨率下使用相同长度的嵌入能够和图像检索任务最好的技术相当。

引言

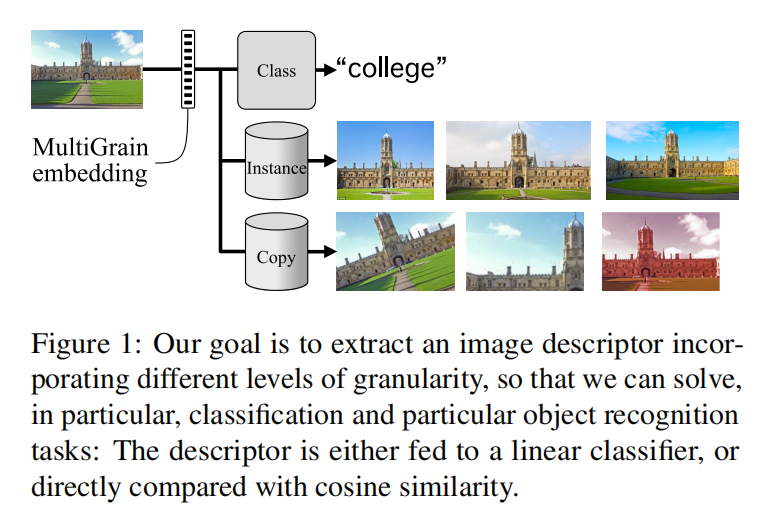
论文主要贡献：

介绍了MultiGrain架构，它输出一个包含不同粒度级别的特征的图像嵌入表示。另外使用基于分类和检索的目标函数能够提升分类性能；
性能提升的部分原因来自于批量策略，为了检索损失计算，在每个批次中包含了经过数据增强的重复图像；
架构中包含了一个池化层GeM（generalized mean pooling/广义平均池化，来自于图像检索任务）。当使用高分辨率图像时，它能够显著提升分类性能。

架构

论文提出的MultiGrain同时适用于图像分类和实例检索任务。通常来说这两个任务的训练和模型架构均存在极大不同，见下表一所示：

主要集中在5个方面，论文详细描述了这些方面的差异性，并提出MultiGrain实现的方式。

空间池化

池化操作分为两种：

局部空间池化：位于卷积层之间，目的是减少特征图空间分辨率。通常使用最大池化算子，能够保证局部特征的平移不变性；
全局空间池化：位于卷积网络末尾，将3D大小的卷积特征转换成为向量。

分类和检索任务主要差异在于最后的全局池化层设置：

对于分类任务而言，
1. 早期模型（LeNet-5/AlexNet）的空间池化操作仅是将激活特征线性化，因此对于特征位置非常敏感；
2. 最新的架构（ResNet/DenseNet）使用平均池化操作，提供了更全局的平移不变性。
对于检索任务而言，需要更多的局部几何信息：虽然特定目标在视觉上非常相似，但容易受到环境干扰，并且通常情况下查询图像并没有特定的训练数据。所以最后的全局池化层需要提供更多的局部信息。

在MultiGrain中，分类和检索任务共享同一个卷积主干网络。对于最后的全局池化层，论文采用了广义平均池化算子（generalized mean pooling operator/GeM operator）。

假定卷积特征张量，其中表示特征通道数，和分别是特征图的宽和高。使用表示特征图的像素空间位置，所以表示某一个通道上的像素大小：。广义均值池化层（GeM）计算张量中每个通道的广义均值，计算如下：

$$
e=[(\frac{1}{\left| \Omega \right|}\sum_{u\in \Omega} x^{p}{cu})^{\frac{1}{p}}]{c=1,…,C}
$$

其中是一个超参数，表示增加池化特征的对比度，更加聚焦于图像的显著特征。当时，GeM等同于平均池化，当时，它等同于空间最大池化算子。

损失函数

MultiGrain使用的损失函数同时结合了分类任务损失和检索任务损失，如下图2所示。

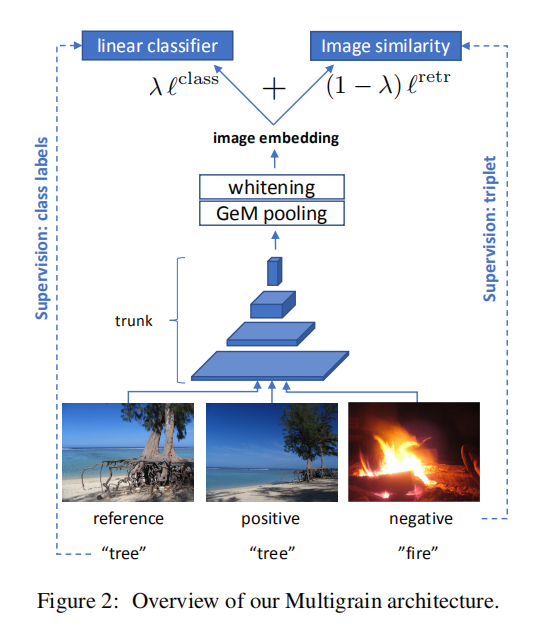
分类损失

MultiGrain使用交叉熵损失进行分类任务训练。假定图像经过卷积网络计算得到的特征为；线性分类器的权重为；共有个类别，表示该图像的真值标签。交叉熵损失（简化版本）计算如下：

其中

检索损失

对于图像检索任务而言，正样本对的相似度距离应该比负样本对的更小。存在两种计算方式，

对比损失（contrastive loss）：正样本对的相似度距离应该低于一个阈值，而负样本对应该高于；
三元组损失（triplet loss）：锚点图像和正样本之间的距离应该低于锚点图像和负样本之间的距离。

论文参考了Sampling matters in deep embedding learning提出的实现方式，给定一批图像，计算图像嵌入向量，归一化到单位球面（unit sphere）；然后采样负样本对计算嵌入向量相似度；最后使用边界损失（margin loss）进行计算。详细实现如下：

给定同一批次的图像，计算嵌入向量。边界损失计算如下：

其中

表示归一化后的嵌入向量之间的欧式距离；
如果是正样本对，那么标签，否则，；
是一个常量超参数，表示边界值；
是一个可学习参数，控制了嵌入向量占据嵌入空间的体积（不懂。。。）。

经过归一化之后，嵌入向量对的距离计算等同于余弦相似度，加上后续的白化操作，就可以作用于检索任务。

论文还描述了正负样本对采样的概率，需要进一步结合源码

联合训练架构

MultiGrain的目标函数联合了分类损失和检索损失，使用因子进行加权训练。对于批量为的输入图像，联合损失计算如下：

批量采样

论文提出一种新型采样策略，称之为repeated augmentations（重复增强策略）。每批次图像共张，首先从分类数据集中采样张训练数据，然后使用扩充策略重复次，组成该批次训练数据。对于检索任务而言，表示图像和图像是相同图像进行扩充得到的。

论文推测使用RA能够促进网络学习重复图像之间的不变特征。

PCA白化

。。。

输入分辨率

对于分类任务而言，通常将图像进行裁剪并缩放到较低的分辨率（比如大小），这种方式可以保证较低的内存占用，更快速的推理以及批处理训练。而对于检索任务而言，更依赖于图像目标的精细细节，通常将图像等比缩放到800或者1024，并且不执行裁剪。

MultiGrain可以实现以较低的分辨率同时训练分类和检索网络；然后在推理阶段，使用较高分辨率来提高检索任务性能。关键在于GeM的使用，在训练阶段，使用池化指数和分辨率；在推理阶段，使用更大的分辨率$s^{}>s $时，可以使用一个更大的池化指数$ p^{}>p$来提升性能。

论文还提出了一个代理任务来计算不同输入分辨率下池化指数的选择。从ImageNet中采样2000张图像（每类2张图片），然后使用扩充策略创建另外5张副本。

使用上面提到的损失函数训练代理数据集，然后评估不同分辨率和池化指数下查询图像的检索精度，类似于UKBench，计算top-5排序中扩充副本的个数。实现结果如下：

实验

设置

基础架构以及训练设置

网络主干：ResNet-50
优化器：SGD
训练轮数：120
学习率调度：初始0.2，第30/60/90轮衰减0.1
批量大小：512
每一轮固定训练次数：
单批次扩充个数：

数据扩充

左右翻转（flip）
随机缩放裁剪（random resized crops）
随机照明噪声（random lighting noise）
亮度、对比度和饱和度的颜色抖动（color jittering of brightness, contrast and saturation）

论文将上述数据预处理操作组合成full扩充策略，如下表所示：

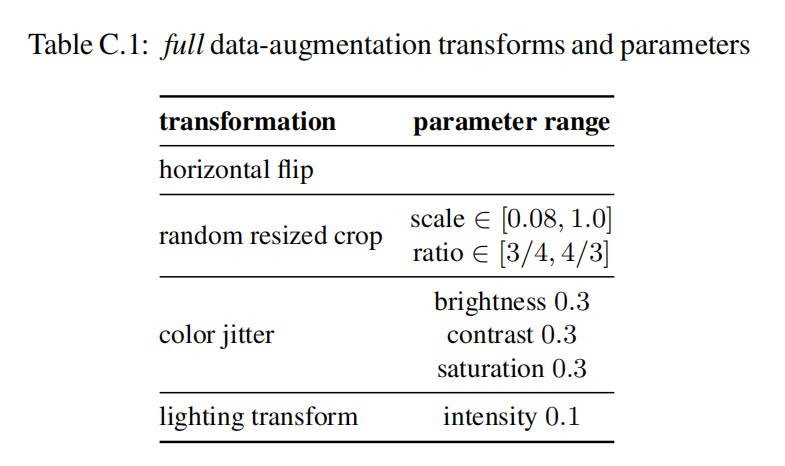
池化指数

在端到端的训练中，论文设置了两组池化指数：和。其中等同于平均池化，这是分类网络常用的设置，而通过实验证明能够提高检索任务性能。如下图3所示，

输入大小和裁剪策略

在训练阶段，MultiGrain使用大小裁剪图像；在测试阶段，论文尝试了3种分辨率设置：，

对于，遵循分类任务评估，将图像最小边缩放到256大小，然后中央裁剪大小；
对于，遵循检索任务评估，将图像最大边缩放至对应大小，然后不需要裁剪，直接输入网络计算。

边界损失和批量采样策略

对于批量采样，设置，每一轮图像扩充3次；对于边界损失，其超参数设置如下表所示：

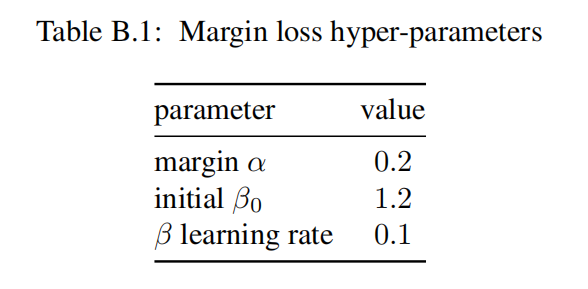
数据集

在训练阶段，使用ImageNet-2012作为训练集，它包含120w张图像，共1000个目标类别。在测试阶段，

对于分类任务，使用ImageNet验证集，它包含了5w张图像；
对于检索任务，使用Holidays/UKB/INRIA Copydays。

对于PCA白化参数，从YFCC100M中提取出2w张图像进行计算

扩展输入分辨率以及GeM指数

论文在训练阶段使用大小，基于RA采样策略，同时设置池化指数。在测试阶段，同样使用分辨率，能够实现76.9% top-1分类精度，比非RA训练高0.7%。

论文尝试了输入更大图像$s^{}> 224 $进行测试，并且变化池化指数$ p^{}\neq p=3$。结果如下图4所示，分别报告了在ImageNet验证集上的分类精度和在Holidays上的检索精度：

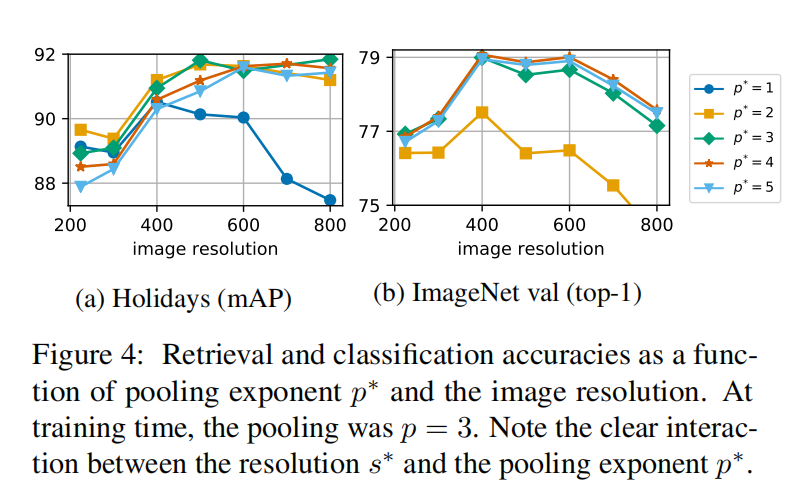
可以观察到当使用更大尺度的$s^{} $的时候，同样需要提高池化指数$ p^{}$的个大小。

平衡参数的分析

论文分析了损失函数超参数的影响，如下图5所示：

从梯度分析来看，随着训练轮数的增加，分类损失逐渐的占据了主导地位。最终论文选择设置，这个结果是基于测试集评估的。

分类任务结果

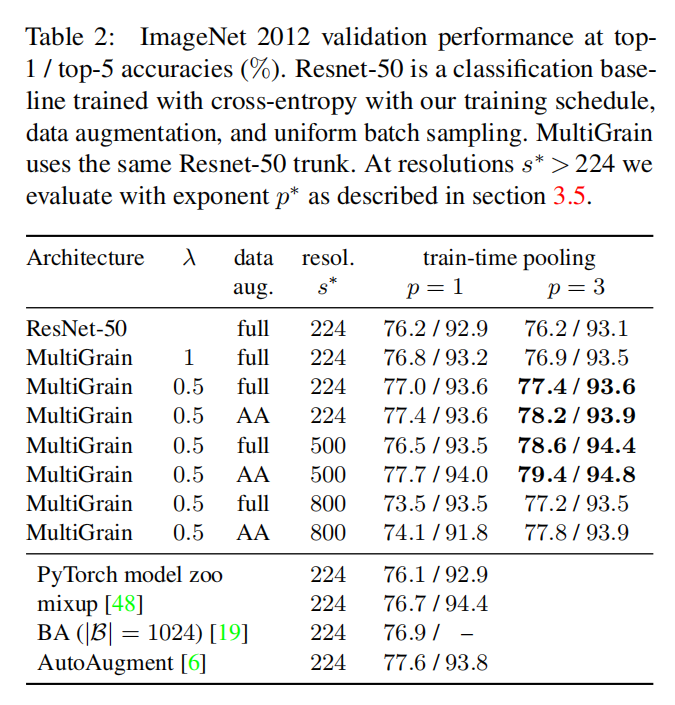
如上表2所示，对于ResNet-50的测试结果（p=1, s=224，使用full数据扩充策略，得到获得76.2% top-1精度），MultiGrain获得了78.6% top-1精度（p=3, $\lambda=0.5$, s=50）。论文将提升划分为4个部分：

RA策略提升了+0.6%(p=1)
边界损失提升了+0.2%(p=1)
提供了+0.4%
提高分辨率到500提升了+1.2%

AutoAugment

将AutoAugment集成到数据扩充，设置每一轮训练7508批次，最终获得79.4% top-1精度（）。

检索任务结果

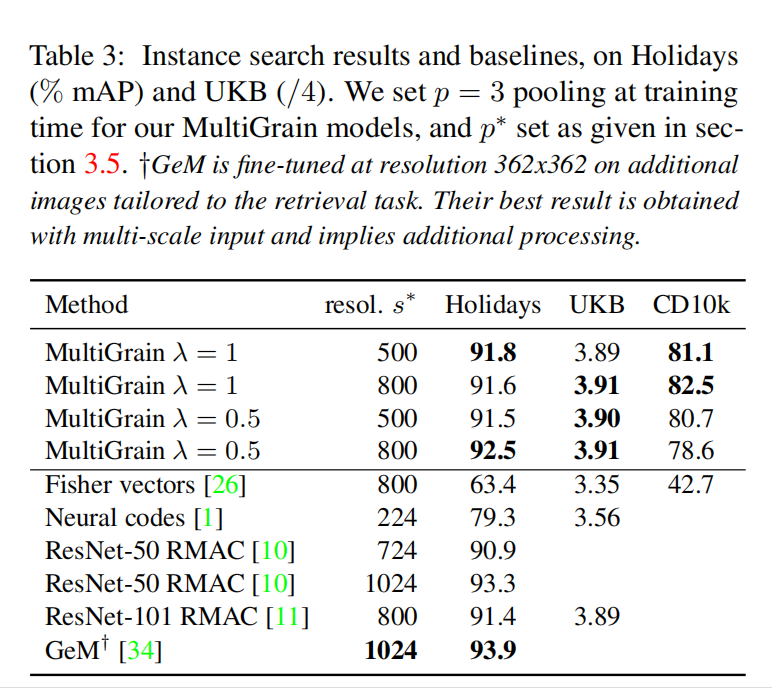
从检索任务来看，其训练性能并不突出，并且使用了高分辨率输入（），实用性一般。

小结

MultiGrain架构由分类卷积网络主干 + GeM池化层 + 分类head/检索head组成。在训练阶段，使用较低分辨率以及RA采样策略，联合分类损失和检索损失共同训练；在测试阶段，使用较高分辨率以及变化池化指数提升分类精度。

从测试结果来看，MultiGrain获得的提升很大一部分来自于图像分辨率增大以及AutoAugment的使用。它也是首次将GeM应用到了分类任务，并且分析了增大分辨率和增大池化指数对于分类精度的有效性。总的来说，MultiGrain更适用于分类任务。当然，它提出的RA采样策略以及联合损失设计能够帮助到实际检索任务中数据的处理和训练。