数据结构-图5

发表于 2019-08-18 更新于 2025-12-16 分类于技术教程，项目实践，基础教程，算法复现阅读次数：本文字数： 2.4k 阅读时长 ≈ 9 分钟

学习路径如下：

完整工程：zjZSTU/GraphLib

最小生成树

最小生成树

给定无向图，代表连接顶点和的边，代表此边的权重，如果存在生成树使得最小（权值之和最小），那么称为最小生成树(MST, Minimum Spanning Tree)

有两种方式常用于最小生成树的创建，一是普里姆（prim）算法，二是克鲁斯卡尔（kruscal）算法

普里姆算法

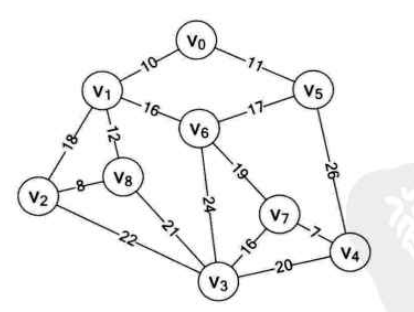
假设是连通网，是上最小生成树中边的集合。算法从开始。重复执行下述操作：在所有的边中找一条代价最小的边并入集合，同时并入，直至为止。此时中必有条边，则为的最小生成树

因为最小生成树包含连通网所有的顶点，所以从哪个顶点开始都可以
创建一维数组lowcost，表示边集TE的最小权值数组。数组下标表示顶点
- 如果该顶点未加入最小生成树，则成员值表示该顶点的边权值，符合条件：所连接的另一个顶点在最小生成树中
- 如果已加入最小生成树，设置为-1
创建一维数组adjvex，表示最小生成树T的边集TE
- 数组下标表示顶点，成员值表示另一个顶点
- 两个顶点之间的边权值保存在lowcost对应下标中

Prim算法对顶点进行展开，每次添加一个顶点到MST，难点在于如何找到符合条件的顶点：

初始化时可以随机选择一个顶点加入MST（通常选顶点0）。遍历其他顶点
- 如果其他顶点与顶点0存在边，则权值加入lowcost，adjvex对应下标值设置为0（表示顶点0）
- 如果其他顶点与顶点0不存在边，则lowcost对应下标设置为最大值，adjvex对应下标也设置为0
遍历n-1轮（n表示顶点数）
- 每一轮都从lowcost中选择一条最小权值边（不包含值为-1的下标），将指定下标加入MST（lowcost对应下标值设置为-1）
- 遍历每次新加入最小生成树T的顶点所连接的边，如果符合条件（另一个顶点不再T中，通过判断lowcost对应下标值是否为-1），与lowcost相应位置权值进行比较，邻接顶点及其权值加入adjvex和lowcost中

c++实现

分别使用邻接矩阵和邻接表实现普里姆算法

邻接矩阵

void AdjacencyMatrixUndirectedGraph::MiniSpanTree_Prim(MGraph G) {
    int min, i, j, k;
    std::array<int, MAXVEX> adjvex = {};
    std::array<int, MAXVEX> lowcost = {};

    // 最先添加顶点0到MST中
    // adjvex赋值为边的另一个顶点值， 如果顶点已在MST中，指定下标赋值为-1
    int begin_vex = 0;
    adjvex[begin_vex] = 0;
    lowcost[begin_vex] = -1;
    for (i = 1; i < G.numVertexes; i++) {
        lowcost[i] = G.arcs[0][i];
        adjvex[i] = 0;
    }

    int weight = 0;
    // 遍历n-1轮，得到另外的顶点
    for (i = 1; i < G.numVertexes; i++) {
        min = GINFINITY;
        // 遍历n-1次，搜索最小权值边
        j = 1, k = 0;
        while (j < G.numVertexes) {
            if (lowcost[j] != -1 and lowcost[j] < min) {
                min = lowcost[j];
                k = j;
            }
            j++;
        }

        // 输出最小权值边
        printf("(%d, %d) %d\n", adjvex[k], k, lowcost[k]);
        weight += lowcost[k];
        // 顶点k已加入MST，lowcost赋值为-1
        lowcost[k] = -1;

        // 比较顶点k的边集和MST的最小权值边集，进行替换
        for (j = 1; j < G.numVertexes; j++) {
            if (k != j and lowcost[j] != -1 and G.arcs[k][j] < lowcost[j]) {
                lowcost[j] = G.arcs[k][j];
                adjvex[j] = k;
            }
        }
    }
    cout << "最小权值为：" << weight << endl;
}

邻接表

void AdjacencyTableUndirectedGraph::MiniSpanTree_Prim(GraphAdjList G) {
    int min, i, j, k;
    EdgeNode *e;
    std::array<int, MAXVEX> adjvex = {};
    std::array<int, MAXVEX> lowcost = {};

    // 初始化
    for (i = 0; i < G.numVertexes; i++) {
        lowcost[i] = GINFINITY;
        adjvex[i] = 0;
    }

    // 默认添加顶点0到MST
    // adjvex赋值为边的另一个顶点值， 如果顶点已在MST中，指定下标赋值为-1
    int begin_index = 0;
    adjvex[begin_index] = 0;
    lowcost[begin_index] = -1;
    e = G.adjList[begin_index].firstEdge;
    while (e != nullptr) {
        lowcost[e->adjvex] = e->weight;
        adjvex[e->adjvex] = 0;

        e = e->next;
    }

    int weight = 0;
    // 遍历n-1轮，得到另外的顶点
    for (i = 1; i < G.numVertexes; i++) {
        min = GINFINITY;
        // 遍历n-1次，搜索最小权值边
        j = 1, k = 0;
        while (j < G.numVertexes) {
            if (lowcost[j] != -1 and lowcost[j] < min) {
                min = lowcost[j];
                k = j;
            }
            j++;
        }

        // 输出最小权值边
        printf("(%d, %d) %d\n", adjvex[k], k, lowcost[k]);
        // 顶点k已加入MST，lowcost赋值为-1
        weight += lowcost[k];
        lowcost[k] = -1;

        // 比较顶点k的边集和MST的最小权值边集
        e = G.adjList[k].firstEdge;
        while (e != nullptr) {
            if (lowcost[e->adjvex] != -1 and e->weight < lowcost[e->adjvex]) {
                lowcost[e->adjvex] = e->weight;
                adjvex[e->adjvex] = k;
            }

            e = e->next;
        }
    }
    cout << "MST权值和为：" << weight << endl;
}

克鲁斯卡尔算法

假设是连通网，则令最小生成树的初始状态为只有个顶点而无边的非连通图，图中每个顶点自成一个连通分量。在中选择代价最小的边，若该边依附的顶点在中的不同分量上，则将此边加入到中，否则舍去此边而选择下一条代价最小的边。依次类推，直至中所有顶点都在同一个连通分量上为止

对边集按权重值进行排序，升序搜索，保证得到符合条件的边以及顶点
判断边连接的顶点是否位于不同分量

Prim算法对边进行展开，每次添加一个边到MST，难点在于如何找到符合条件的边（如何判断两个顶点位于不同分量）：

定义结构体Edge，保存边权值和两个顶点（区分边起点和边终点）
定义一维数组edges，类型为Edge，保存每条边信息，并按权值进行升序排序
定义一维数组parent，表示最小生成树的边集，数组下标表示一个顶点，成员值表示另一个顶点
遍历所有边
- 初始时所有成员值均为0，表示每个顶点属于一个单独分量
- 假定第一条边的起始顶点为2，终止顶点为8，那么设置parent[2]=8，表示连接边2->8
- 假定第二条边的起始顶点为4，终止顶点为8，那么设置parent[4]=8，表示连接边4->8
- 假定第三条边的起始顶点为2，终止顶点为4，由上面两条边的设置可知，顶点2和4在同一个分量中
- 设置函数Find，输入起始下标f和数组parent，如果该下标成员值大于0（表明有边相连），将该成员值设为起始下标f，继续遍历，返回最后的f
- 通过Find遍历边的两个顶点所在的分量，得到返回值n和m
  - 如果返回下标值一致，那么属于同一个分量，舍弃该边
  - 如果返回下标值不同，那么两个顶点属于不同的分量。设置parent[n]=m，连接两个分量，并保证下次遍历时得到的最后顶点均为m

c++实现

分别使用邻接矩阵和邻接表实现克鲁斯卡尔算法

邻接矩阵

// 权值边存储结构
typedef struct {
    int begin;
    int end;
    int weight;
} Edge;

void AdjacencyMatrixUndirectedGraph::MiniSpanTree_Kruskal(MGraph G) {
    int i, j, k, n, m;
    std::array<Edge, MAXEDGE> edges = {};
    // 保存最小生成树，数组下标表示一个顶点，赋值表示另一个顶点
    std::array<int, MAXEDGE> parent = {};

    // 将边集赋值给edges
    k = 0;
    for (i = 0; i < G.numVertexes; i++) {
        for (j = i + 1; j < G.numVertexes; j++) {
            if (G.arcs[i][j] != GINFINITY) {
                Edge edge;
                edge.begin = i;
                edge.end = j;
                edge.weight = G.arcs[i][j];

                edges[k] = edge;
                k++;
            }
        }
    }
    // 按权值升序排序
    std::sort(edges.begin(), edges.begin() + G.numEdges, less_second);

    int weight = 0;
    // 遍历所有边，
    for (i = 0; i < G.numEdges; i++) {
        n = Find(parent, edges[i].begin);
        m = Find(parent, edges[i].end);
        // 判断两个分量是否同属一个
        if (n != m) {
            parent[n] = m;
            printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
            weight += edges[i].weight;
        }
    }
    cout << "MST权值和为：" << weight << endl;
}

bool AdjacencyMatrixUndirectedGraph::less_second(Edge x, Edge y) {
    return x.weight < y.weight;
}

int AdjacencyMatrixUndirectedGraph::Find(std::array<int, MAXEDGE> &parent, int f) {
    // 遍历分量
    while (parent[f] > 0) {
        f = parent[f];
    }

    return f;
}

邻接表

void AdjacencyTableUndirectedGraph::MiniSpanTree_Kruskal(GraphAdjList G) {
    int i, j, k, n, m;
    EdgeNode *e;
    std::array<Edge, MAXEDGE> edges = {};
    // 保存最小生成树，数组下标表示一个顶点，赋值表示另一个顶点
    int parent[MAXVEX] = {};

    // 将边集赋值给edges
    k = 0;
    for (i = 0; i < G.numVertexes; i++) {
        e = G.adjList[i].firstEdge;

        while (e != nullptr) {
            if (e->adjvex > i) {
                Edge edge;
                edge.begin = i;
                edge.end = e->adjvex;
                edge.weight = e->weight;

                edges[k] = edge;
                k++;
            }

            e = e->next;
        }
    }
    // 按权值升序排序
    std::sort(edges.begin(), edges.begin() + G.numEdges, less_second);

    int weight = 0;
    // 升序遍历
    for (i = 0; i < G.numEdges; i++) {
        n = Find(parent, edges[i].begin);
        m = Find(parent, edges[i].end);
        // 判断两个分量是否同属一个
        if (n != m) {
            parent[n] = m;
            printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
            weight += edges[i].weight;
        }
    }
    cout << "MST权值和为：" << weight << endl;
}

bool AdjacencyTableUndirectedGraph::less_second(Edge x, Edge y) {
    return x.weight < y.weight;
}

int AdjacencyTableUndirectedGraph::Find(int *parent, int f) {
    // 遍历分量
    while (parent[f] > 0) {
        f = parent[f];
    }

    return f;
}

小结

普里姆算法针对顶点进行展开，每次选择一个顶点进入最小生成树，对于稠密图而言效率更高
克鲁斯卡尔算法针对边进行展开，每次选择一条边连接两个不同分量，对于稀疏图而言效率更高

最小生成树

普里姆算法

c++实现

邻接矩阵

邻接表

克鲁斯卡尔算法

c++实现

邻接矩阵

邻接表

小结

相关阅读