Cross-dimensional Weighting for Aggregated Deep Convolutional Features

发表于 更新于 分类于
本文字数： 5.4k 阅读时长 ≈ 10 分钟

原文地址：Cross-dimensional Weighting for Aggregated Deep Convolutional Features

官方实现：YahooArchive/crow

复现地址：zjykzj/crow-pytorch

摘要

We propose a simple and straightforward way of creating powerful image representations via cross-dimensional weighting and aggregation of deep convolutional neural network layer outputs. We first present a generalized framework that encompasses a broad family of approaches and includes cross-dimensional pooling and weighting steps. We then propose specific non-parametric schemes for both spatial- and channel-wise weighting that boost the effect of highly active spatial responses and at the same time regulate burstiness effects. We experiment on different public datasets for image search and show that our approach outperforms the current state-of-the-art for approaches based on pre-trained networks. We also provide an easy-to-use, open source implementation that reproduces our results.

我们提出了一种简单直接的方法，通过深度卷积神经网络层输出的跨维加权和聚合来创建强大的图像表示。我们首先提出了一个通用框架，它包含了一个广泛的实现并且包括了跨维度的池化和加权步骤。然后，我们提出了针对空间和通道加权的特定非参数方案，在提升高度活跃的空间响应效果的同时能够调节突发效应。我们在不同的公共数据集上进行图像搜索实验，结果表明我们的方法优于当前最先进的基于预训练网络的方法。我们还提供了一个易于使用的开源实现来复现我们的结果。

引言

卷积神经网络在图像检索任务上的应用从全连接层输出特征转移到卷积层输出特征，这样做的好处是：输入数据可以是任意大小，可以避免训练过程对原始图像进行裁剪或者缩放，保留了原始数据的空间特性。论文在最后一个卷积层输出的基础上执行逐空间位置加权和逐通道加权，最后逐通道执行求和池化（聚合）操作。将最后输出的特征称为跨维度加权和池化特征（ cross-dimensional weighting and pooling as CroW features）。

论文主要贡献：

  1. 提出一个通用的卷积特征聚合框架，将卷积特征生成划分为各个步骤，包括跨维度加权以及池化步骤；
  2. 提出一个无参数的加权方式，对卷积特征执行跨空间位置（提升已高度激活的空间响应影响力）和跨通道（调节通道突发的影响）加权；
  3. 在图像搜索数据集上展示了最好的结果，不需要执行任何微调操作。

卷积特征聚合框架

框架概述

  • 第一步：执行空间局部池化
    • 如果卷积特征太大，可以先进行空间局部池化操作，比如最大池化或者平均池化；
    • 池化层滤波器感受野大小为\(w\times h\)，步长为\(s\)；
    • 极端情况下
      • 执行全局池化（感受野大小为每个通道空间尺寸）；
      • 执行\(1\times 1\)大小池化（就是没有这一步局部池化操作）；
  • 计算空间加权因子
    • 每个特征图中特定位置\((i,j)\)赋予一个权重\(\alpha_{i,j}\)；
    • 注意：每个通道特征图上相同位置的权重值大小一致；
  • 计算通道加权因子
    • 对于每个通道\(k\)，赋值一个加权因子\(\beta_{k}\)；
  • 执行加权求和聚合
    • 结合前两步计算的空间加权因子\(\alpha_{i,j}\)和通道加权因子\(\beta_{k}\)，基于每个通道执行加权求和操作，将张量特征转换为一维向量；
  • 执行向量归一化
    • 对计算得到的特征向量执行归一化操作（比如L1/L2归一化）；
  • 执行维度衰减
    • 减少归一化向量的维度，使用比如PCA，同时还可以执行譬如白化等逐维度缩放操作；
  • 执行最后归一化
    • 再次进行归一化操作，输出最终的特征向量

跨维度加权

假定卷积网络第\(l\)层输出的3维特征张量大小为\(X\in R^{(K\times W\times H)}\)，在\(X\)中第\(k\)个维度特征图，位置为\((i,j)\)的特征大小为\(X_{kij}\)。为了便于使用，定义\(X\)的通道矩阵为\(C^{(k)}\)，其中\(C^{(k)}_{ij}=X_{kij}\)；类似的，定义空间位置\((i,j)\)的通道响应向量为\(\lambda^{(ij)}\)，其中\(\lambda^{(ij)}_{k}=X_{kij}\)

对特征向量\(X\)应用逐通道权重\(\beta_{k}\)和逐空间权重\(\alpha_{ij}\)，加权特征向量\(X^{'}\)的计算方式如下

\[ X^{'}_{kij}=\alpha_{ij}\beta_{k}X_{kij} \]

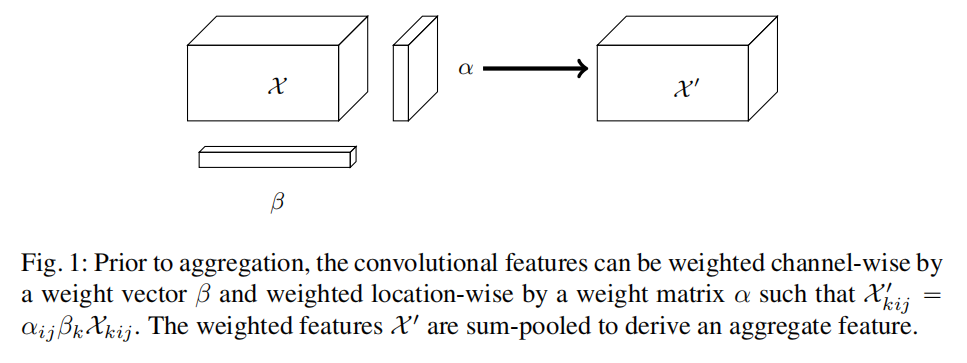
完成跨维度加权操作后，对每个通道执行求和操作得到聚合特征向量\(F=\{f_{1}, ..., f_{k}\}\)：

\[ f_{k}=\sum_{i=1}^{W}\sum_{j=1}^{H}X^{'}_{kij} \]

完成上述聚合操作后，遵循之前论文的最佳实践：对\(F\)执行\(L2\)归一化操作，然后执行白化操作，最后再次执行\(L2\)归一化操作。论文把从上述特征聚合框架中得到的特征向量称为跨维度加权（Cross-dimensional Weighted, Crow）特征。

特征加权实现

上一节概述了通用的特征聚合步骤以及论文提出的CroW特征实现架构。在这一节详细描述空间加权因子计算方案（基于卷积层输出特征的空间激活）以及通道加权因子计算方案（基于通道稀疏性）

空间加权

假定\(S^{'}\in R^{(W\times H)}\)表示逐通道响应矩阵（就是每个空间位置累加所有通道值），其计算方式如下：

\[ S^{'}=\sum_{k}C^{(k)} \]

对\(S^{'}\)进行归一化以及响应缩放（power-scaling）操作得到聚合后的空间响应特征图\(S\)，其每个空间位置\((i,j)\)的计算如下：

\[ S_{ij}=(\frac{S_{ij}^{'}}{(\sum_{m,n}(S^{'}_{m,n})^{a})^{\frac{1}{a}}})^{\frac{1}{b}} \]

计算得到的聚合特征图\(S\)就是空间加权特征图，\(\alpha_{ij}=S_{ij}\)。论文实验了多种归一化\(S^{'}\)的方式，差异性非常小，最后论文选择了\(L2\)归一化实现，并且设置超参数\(b=2\)。

论文在Paris数据集上可视化了空间加权作用，如下图所示

从上图中可以发现，空间加权因子可以有效提升关键内容并且降低无效内容影响 。尽管光线和视角有很大的变化，但相似的视觉元素在加权因子作用下均得到了增强。

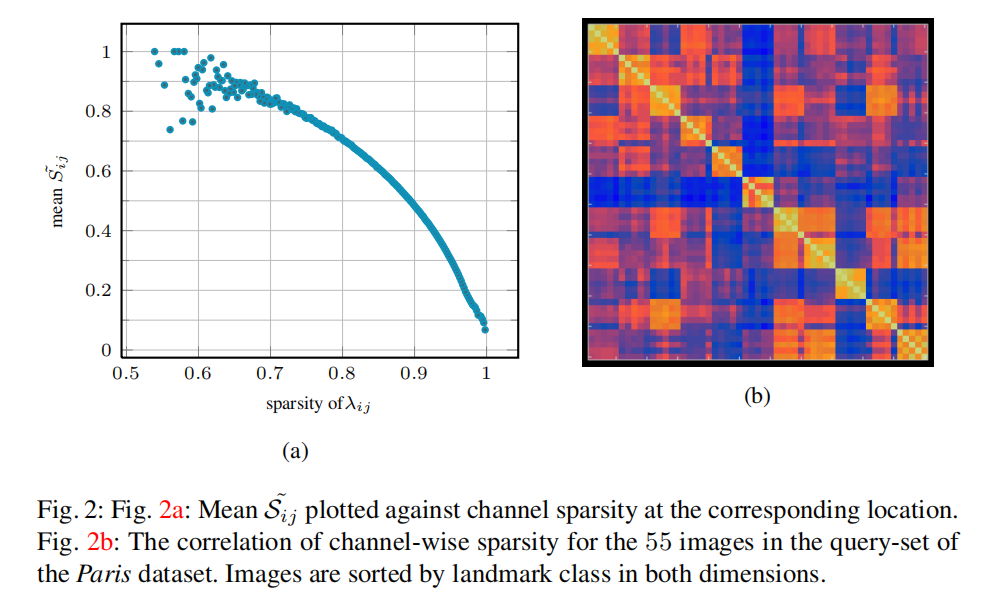
论文还发现了空间权重\(S_{ij}\)和对应通道响应\(\lambda^{(ij)}\)的稀疏性之间的关系。论文在Paris数据集上进行了实验，计算卷积层特征每个空间位置的空间加权因子\(S_{ij}\)，然后基于该空间位置在逐通道中最大的权重执行归一化操作，称为\(\tilde{S}_{ij}\)。统计各个空间位置的稀疏性以及计算\(\tilde{S}_{ij}\)的均值（这个不太理解，是说的所有图像的均值吗？），如下图2a所示：

从上图2a中可以发现，空间加权因子倾向于提升在多个通道已激活的空间位置。

通道加权

论文基于特征图稀疏性执行通道加权，对于相似图像，其输出特征同样存在相似性。假定对于每个通道\(k\)，\(Q_{k}\)表示每个空间位置上逐通道非零响应的比例，从而计算得到逐通道稀疏性（per-channel sparsity）\(E_{k}\)如下：

\[ E_{k}=1-Q_{k} \]

其中\(Q=\frac{1}{WH}\sum_{ij} 1[\lambda^{(ij)}\gt 0]\)。论文基于Paris查询集，可视化了不同图像的通道稀疏性向量之间的相关性。查询集共有55张图像，划分为11类，也就是每类5张图像。按类别进行排序，计算两两图像通道稀疏性向量之间的相关性，如上图2b所示。可以发现对于相同建筑图像，其通道稀疏性\(E\)存在高度相关性，这说明了通道稀疏性包含了关键的判别信息。

论文在聚合阶段执行逐通道求和池化操作，这种情况下，不频繁出现的特征也能够提供重要信号。例如，某个特征会持续出现在同一类别某些图像中，尽管出现的次数很少，但也会帮助同类图像检索。论文参考inverse document frequency实现了新的通道加权方式，通过逐通道权重来提升稀有特征在整体响应中的贡献：

\[ L_{k} = log(\frac{K\varepsilon +\sum_{h}Q_{h}}{\varepsilon +Q_{k}}) \]

  • \(\varepsilon\)是一个极小的常数，为了数值稳定性。

在具体实现中，其数学公式更类似于：

\[ L_{k} = log(\frac{\sum_{h}Q_{h}}{\varepsilon +Q_{k}}) \]

论文在下图4中显示了拥有最高稀疏敏感性通道权重（ sparsity-sensitive channel weights, SSW）的通道中非零空间位置对应的感受野

CroW vs. uCroW vs. SPoC

  • uCroW：对通道和空间加权因子赋予相同的权重大小，然后执行逐通道求和池化操作。这种特征聚合方式是CroW特征的简化版本，称为uniform CroW, uCroW

CroW、uCroW以及SPoC的关系如下表一所示：

实验

评估协议

数据集

论文使用了4个公共数据集进行实验：

  1. Oxford5k
  2. Paris6k
  3. Oxford5k + Oxford100k（干扰项）
  4. Paris6k + Oxford100k（干扰项）
  5. Holidays

其中，对于Oxford数据集，使用裁剪目标后的图像作为查询集；对于Holidays，使用直立版本图像集。

评估指标

  • 使用mAP(mean average precision)作为评估指标；
  • 使用caffe2作为推理库，基于VGG16预训练模型；
  • 预处理阶段，对图像减去均值。

查询扩展

基于查询图像和数据集图像对之间的相似距离进行降序排序，将查询图像特征与前\(M\)个数据集特征求均值，进行\(L2\)归一化之后再次进行查询，称为查询扩展（query expansion）。查询扩展操作可以进一步提高性能。

初步实验

图像大小/层/特征维度选择

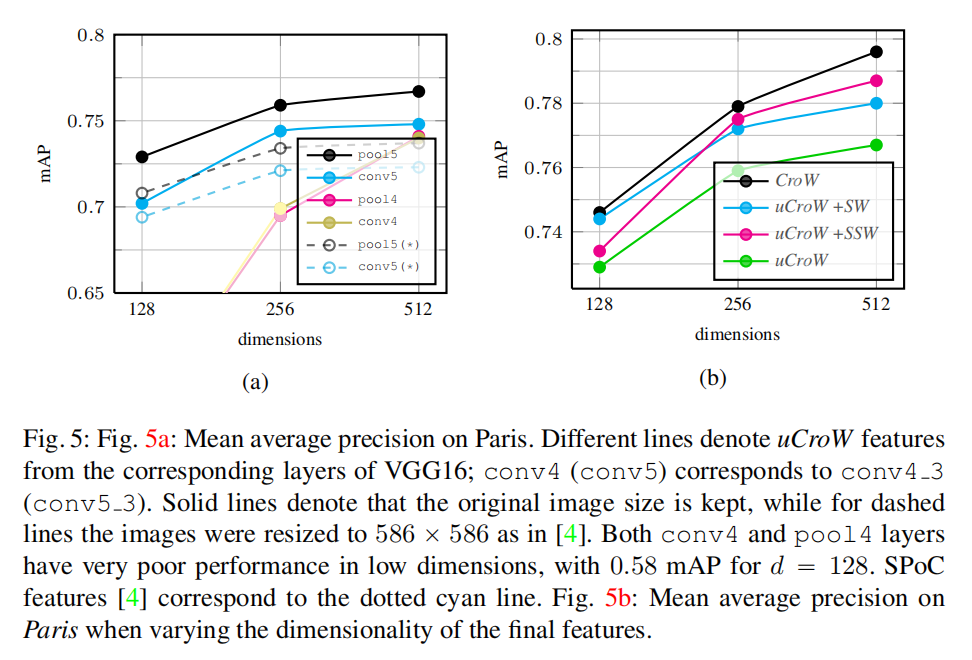
上图5a比较了基于不同层输出以及不同图像输入大小（实线表示保持原始图像大小，虚线表示缩放到\(586\times 586\)）进行特征生成的性能，可以发现

  1. 使用pool5(max pooling)层能够得到最好性能；
  2. 保持图像原始大小能够提升性能。

上图5b比较了逐空间加权以及逐通道加权对于最终性能的影响，另外，从上述两个实验中都可以发现下降特征维度会衰减检索性能。

白化

论文还比较了使用不同数据集进行白化参数学习对于最终评估结果的影响。在下表2中，对于Paris数据集检索，论文尝试了3个不同的数据集（Oxford5k/Holidays/Oxford100k）进行白化参数学习。

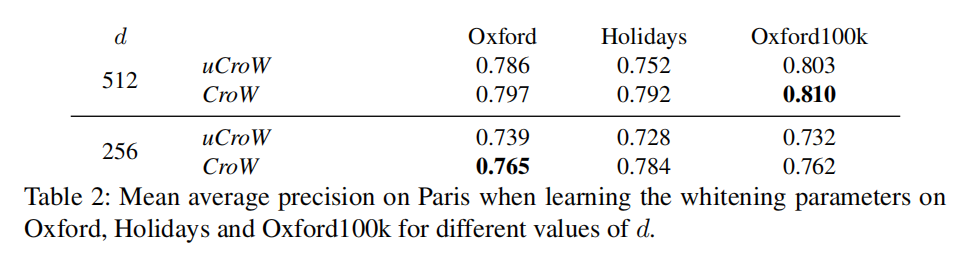
在后续实验中，论文使用Oxford进行Paris的白化参数学习，反之亦然。另外使用Oxford100k作为Holidays数据集的白化参数学习。

图像搜索

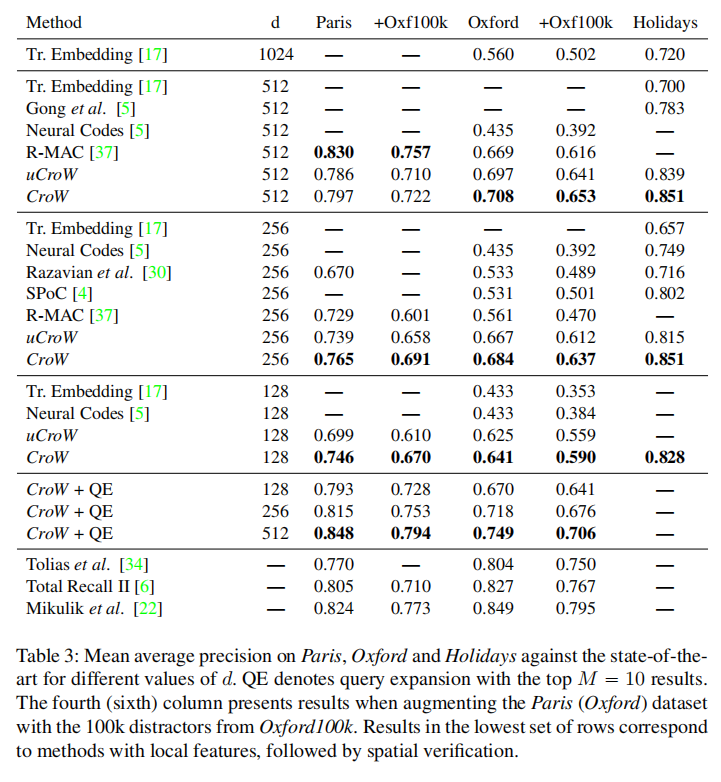
论文在不同数据集上比较了CroW算法与其他算法，可以发现CroW一致性超过了其他算法（除了R-MAC在Paris数据集），并且随着特征维度降低，性能更加强大。

上图6展示了降维特征到32维度之后的图像检索结果，展示了CroW特征对视角和光照变化的不变性，即使在严重压缩后也是如此。

CroW + QE的组合（论文结合了前10个排序结果再次进行查询）能够进一步提升性能。上图7中论文使用512维的CroW特征进行检索，可以发现在P@10中仅出现3个错误，说明了是因为初始排序的结果就已经非常高质量了，所以QE能够提高性能。

小结

论文首先总结过去的实现，提出一个基于卷积神经网络输出特征的通用聚合框架，然后在其中空间加权和通道加权两个阶段提出自己的无参数增强方案，通过实验证明了其有效性。

对于论文强调的原始输入图像大小以及Max Pooling池化操作的有效性，个人认为更多的是基于VGG架构模型的特征，在个人实验中发现不一定适用于其他网络架构。另外对于最后重排序阶段的查询扩展操作，论文也通过图像可视化说明了是因为初始排序的结果就已经非常高质量了，所以再次排序会提高性能。

相关阅读